Implement HDL Optimized SVD for Non-Square Matrix with Scalar Input and Simplified AXI4 Protocol

This example shows how to use the Non-Square Jacobi SVD HDL Optimized block to compute the singular value decomposition (SVD) of non-square matrices. The input data is in scalar format and uses simplified AXI4 protocol. The Non-Square Jacobi SVD HDL Optimized block uses the AMBA AXI handshake protocol for both input and output. The valid/ready handshake process is used to transfer data and control information. For more details about the handshake process, see Non-Square Jacobi SVD HDL Optimized. In certain use cases such as using this block with IP core generation workflow, this block needs to interface with upstream block using the Model Design for AXI4-Stream Interface Generation (HDL Coder). In this example, the sAXI2AXI block serves as an adapter between simplified AXI and AMBA AXI protocols. It also converts the scalar input into row format and feeds into the Non-Square Jacobi SVD HDL Optimized block.

Define Simulation Parameters

Specify the dimension of the sample matrices, the number of input sample matrices, and the number of iterations of the Jacobi algorithm.

m = 16;
n = 8;
numSamples = 3;
nIterations = 10;

Generate Input A Matrices

Use the specified simulation parameters to generate the input matrix A.

rng('default');
A = randn(m,n,numSamples);

The Non-Square Jacobi SVD HDL Optimized block supports both real and complex inputs. Set the complexity of the input in the block mask accordingly.

% A = complex(randn(m,n,numSamples),randn(m,n,numSamples));

Select Fixed-Point Data Types

Define the desired word length.

wordLength = 32;

Use the upper bound on the singular values to define fixed-point types that will never overflow. First, use the fixed.singularValueUpperBound function to determine the upper bound on the singular values.

svdUpperBound = fixed.singularValueUpperBound(m,n,max(abs(A(:))));

Define the integer length based on the value of the upper bound, with one additional bit for the sign, another additional bit for intermediate CORDIC growth, and one more bit for intermediate growth to compute the Jacobi rotations.

additionalBitGrowth = 3;
integerLength = ceil(log2(svdUpperBound)) + additionalBitGrowth;

Compute the fraction length based on the integer length and the desired word length.

fractionLength = wordLength - integerLength;

Define the signed fixed-point data type to be 'Fixed' or 'ScaledDouble'. You can also define the type to be 'double' or 'single'.

dataType = 'Fixed';
T.A = fi([],1,wordLength,fractionLength,'DataType',dataType);
disp(T.A)

[]

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 32
        FractionLength: 23

Cast the matrix A to the signed fixed-point type.

A = cast(A,'like',T.A);

Configure Model Workspace and Run Simulation

model = 'NonSquareJacobiSVDSimplifiedAXIModel';
open_system(model);
fixed.example.setModelWorkspace(model,'A',A,'m',m,'n',n,...
    'nIterations',nIterations,'numSamples',numSamples);
out = sim(model);

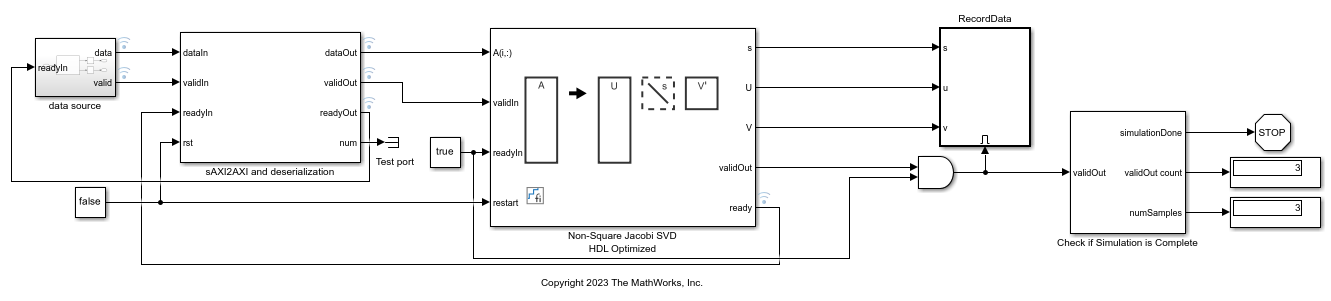
Verify Output Solutions

Verify the output solutions. In these steps, "identical" means within roundoff error.

1. Verify that U*diag(s)*V' is identical to A. relativeErrorUSV represents the relative error between U*diag(s)*V' and A.

2. Verify that the singular values s are identical to the floating-point SVD solution. relativeErrorS represents the relative error between s and the singular values calculated by the MATLAB® svd function.

3. Verify that U and V are unitary matrices. relativeErrorUU represents the relative error between U'*U and the identity matrix. relativeErrorVV represents the relative error between V'*V and the identity matrix.

for i = 1:numSamples
    disp(['Sample #',num2str(i),':']);
    a = A(:,:,i);
    U = out.U(:,:,i);
    V = out.V(:,:,i);
    s = out.s(:,:,i);

    % Verify U*diag(s)*V'
    if norm(double(a)) > 1
        relativeErrorUSV = norm(double(U*diag(s)*V')-double(a))/norm(double(a));
    else
        relativeErrorUSV = norm(double(U*diag(s)*V')-double(a));
    end
    relativeErrorUSV %#ok

    % Verify s
    s_expected = svd(double(a));
    normS = norm(s_expected);
    relativeErrorS = norm(double(s) - s_expected);
    if normS > 1
        relativeErrorS = relativeErrorS/normS;
    end
    relativeErrorS %#ok

    % Verify U'*U
    U = double(U);
    UU = U'*U;
    relativeErrorUU = norm(UU - eye(size(UU))) %#ok

    % Verify V'*V
    V = double(V);
    VV = V'*V;
    relativeErrorVV = norm(VV - eye(size(VV))) %#ok

    disp('---------------');
end

Sample #1:

relativeErrorUSV =

   3.9280e-06


relativeErrorS =

   4.2820e-07


relativeErrorUU =

   2.9636e-07


relativeErrorVV =

   2.3693e-07

---------------
Sample #2:

relativeErrorUSV =

   7.9076e-06


relativeErrorS =

   1.0420e-06


relativeErrorUU =

   3.2885e-07


relativeErrorVV =

   2.9333e-07

---------------
Sample #3:

relativeErrorUSV =

   6.4037e-06


relativeErrorS =

   8.5896e-07


relativeErrorUU =

   3.1438e-07


relativeErrorVV =

   3.0493e-07

---------------