Estimate Vector Autoregression Model Using Econometric Modeler
This example models the quarterly US GDP growth rate, M1 money supply rate, and the 3-month T-bill rate series by using the Econometric Modeler app. The example shows how to perform the following actions in the app:
Stabilize the raw nonstationary series.
Fit several competing vector autoregression (VAR) models, and choose the one with the best, parsimonious fit.
Diagnose each residual series.
Export the chosen model to the command line.
At the command line, the example conducts Granger-causality tests on the series given the estimated model, and it uses the model to generate forecasts.
The data set, which is stored in Data_USEconModel.mat, contains
the raw, quarterly US GDP, M1 money supply, and 3-month T-bill rate, among other
series, from 1947 through 2009.
Load and Import Data into Econometric Modeler
At the command line, load the Data_USEconModel.mat data
set.
load Data_USEconModelAt the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
Import DataTimeTable into the app:
On the Econometric Modeler tab, in the Import section, click the Import button
 .
.In the Import Data dialog box, in the Import? column, select the check box for the
DataTimeTablevariable.Click Import.
GDP, M1SL, and
TB3MS, among other series, appear in the
Time Series pane, and a time series plot containing all
series appears in the figure window.
Create separate time series plots by double-clicking each of
GDP, M1SL, and
TB3MS in the Time Series
pane. Position the Time Series
Plot(series) tabs by clicking and
dragging each to see all plots simultaneously.
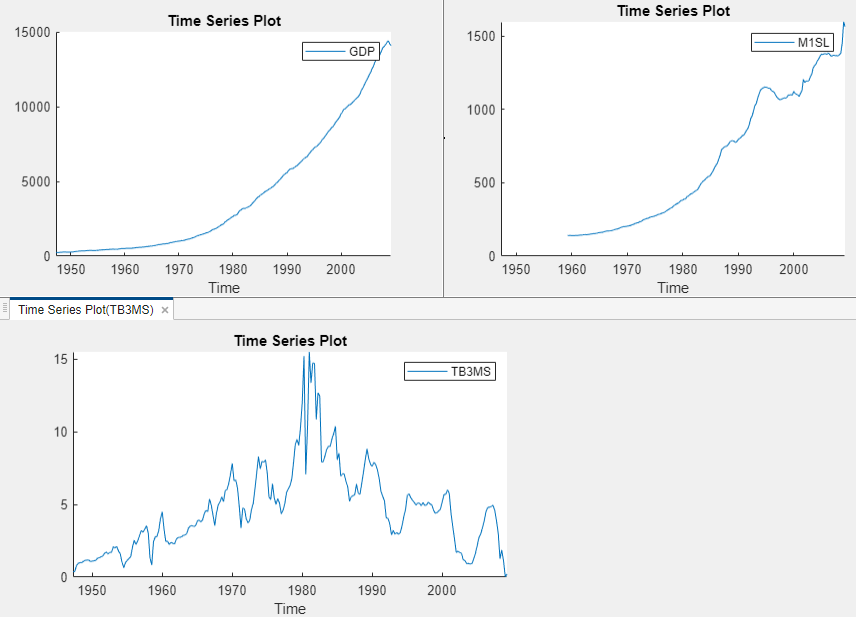
The US GDP and M1 money supply series exhibit exponential growth, and the 3-month T-Bill series appears like a random walk.
Diagnose and Transform Series
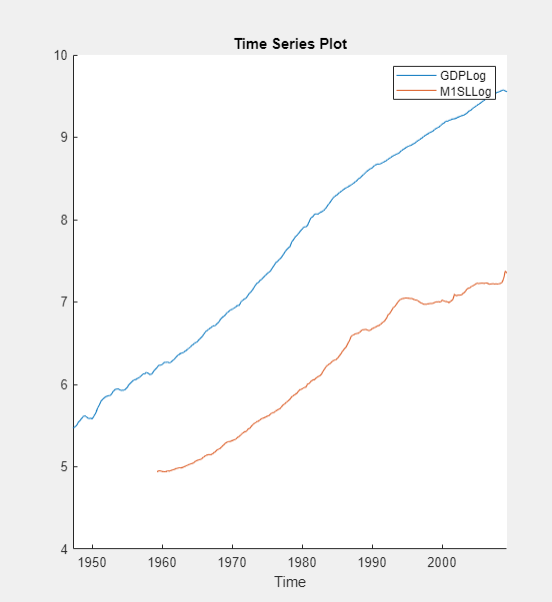
Remove the exponential trend from the GDP and M1 money supply series by
applying the log transform to each series. Click the Econometric
Modeler tab, and then, in the Time Series
pane, click GDP and Ctrl click
M1SL. In the Transforms
section, click Log. The transformed series
GDPLog and M1SLLog
appear in the Time Series pane, and their time series plot
appears in the Time Series Plot(GDPLog) figure
window.
Test the null hypothesis that each series is a unit root process against a
stationary AR(p) with drift alternative, where
p = 4 through 1. For each series
GDPLog, M1SLLog, and
TB3MS:
On the Econometric Modeler tab, in the Time Series pane, click the series.
On the Econometric Modeler tab, in the Time Series pane, click New Test > Augmented Dickey-Fuller Test.
On the ADF tab, in the Parameters section, in the Number of Lags box, type
4. In the Model menu, choose Autoregressive with Drift.In the Tests section, click Run.
Repeat steps 3 and 4 for lags
3,2, and1.
The following figures show the results. The tests fail to reject the null hypotheses of a unit root series in all cases, which suggests that each series is difference stationary.

Stabilize the series by applying the first difference to each series.
Click the Econometric Modeler tab, and then, in the Time Series pane, click
GDPLogand Ctrl+clickM1SLLogandTB3MS.In the Transforms section, click Difference. The transformed series
GDPLogDiff,M1SLLogDiff, andTB3MSDiffappear in the Time Series pane, and their time series plot appears in the Time Series Plot(GDPLogDiff) figure window.Rename
GDPLogDiffandM1SLLogDifftoGDPRateandM1SLRateby clicking their names twice in the Time Series pane, and typing their new names.
Estimate VAR Models
Estimate 3-D VAR(p) models of the US quarterly GDP
growth rate series GDPRate, M1 money supply growth
rate series M1SLRate, and change in the 3-month
treasury bill rate series TB3MSDiff, where
p = 1 through 4.
In the Time Series pane, click
GDPRateand Ctrl+clickM1SLRateandTB3MSDiff.In the Models section, click VAR.
Fit a VAR(1) model (the default) by clicking Estimate in the VAR Model Parameters dialog box.

The model variable
VARappears in the Models pane, its value appears in the Preview pane, and its estimation summary appears in the Model Summary(VAR) document.Repeat steps 1 and 2 for each AR order
p= 2 through 4. In the Var Model Parameters dialog box, set the AR order by using the Autoregressive Order box.Similar to the VAR(1) estimation, a variable for each model (
VAR2,VAR3, andVAR4) appears in the Models pane, and their estimation summaries appear in their respective Model Summary(ModelName) document. You can view properties of an estimated model in the Preview pane by clicking the model in the Models pane. For example, clickVAR4.
Select Model with Best In-Sample Fit
The estimation summary in each Model
Summary(VARp) tab contains a plot
of fitted values and residuals, with respect to the time series in the
Time Series list, a standard statistical table of
estimates and inferences, and a table of information criteria.
Compare the information criteria of each estimated model simultaneously by positioning the estimation summary documents so that they occupy the four quadrants of the right pane. The model with the lowest value has the best, parsimonious fit.
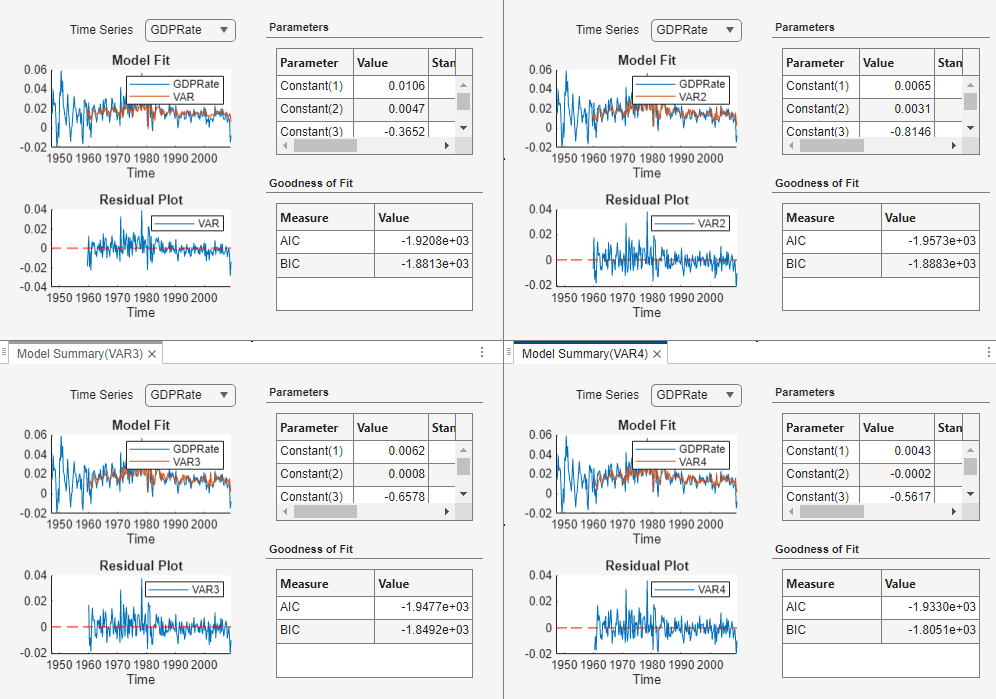
The VAR(2) model VAR2 produces the lowest AIC and
BIC values. Choose this model for further analysis.
Check Goodness of Fit
Inspect the following VAR(2) plots of each residual series:
Histograms, for center, normality, and outliers
Quantile-quantile plots, for normality, skewness, and tails
Autocorrelation function (ACF), for serial correlation
ACF of squared residual series, for heteroscedasticity
This example diagnoses the residuals visually. Alternatively, you can conduct statistical tests to diagnose the residuals.
In the Model Summary(VAR2) document, click Document Actions > Tile All, and then click the Single radio button.
On the Models pane, click
VAR2.
Plot separate residual histograms. On the Econometric Modeler tab, in the Diagnostics section, click Residual Diagnostics > Residual Histogram. Histograms of the each residual series appear in the Histogram(VAR2) document.

Each residual series appears centered around 0, with varying degrees of slight skewness and possible outliers. This example proceeds without addressing possible skewness and outliers.
Plot separate residual quantile-quantile plots. With
VAR2 selected in the Time
Series pane, on the Econometric Modeler tab,
in the Diagnostics section, click Residual
Diagnostics > Residual Q-Q Plot.
Quantile-quantile plots of each residual series appear in the
QQPlot(VAR2) document.
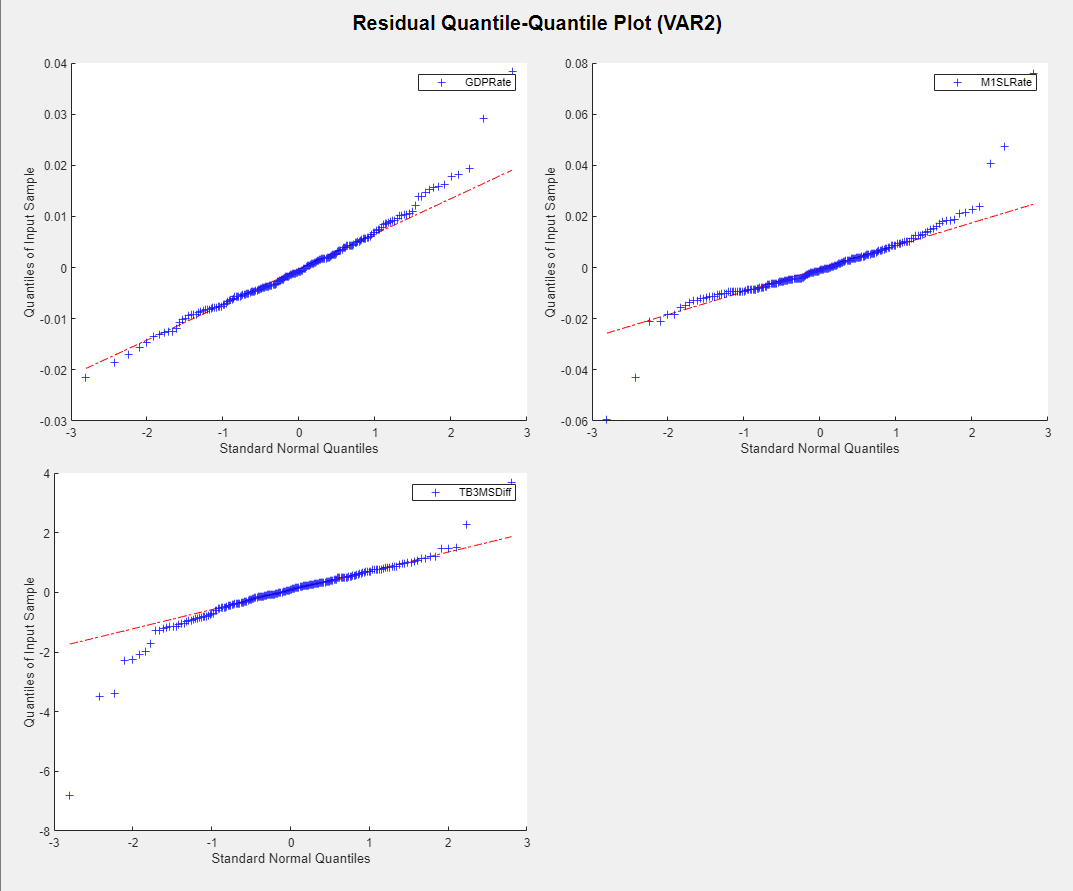
Each series has slightly fatter tails than what is expected by the normal distribution. This example proceeds without addressing possible kurtosis.
Plot separate ACF plots of each residual series. With
VAR2 selected in the Time
Series pane, on the Econometric Modeler tab,
in the Diagnostics section, click Residual
Diagnostics > Autocorrelation
Function. ACF plots of each residual series appear in the
ACF(VAR2) document.
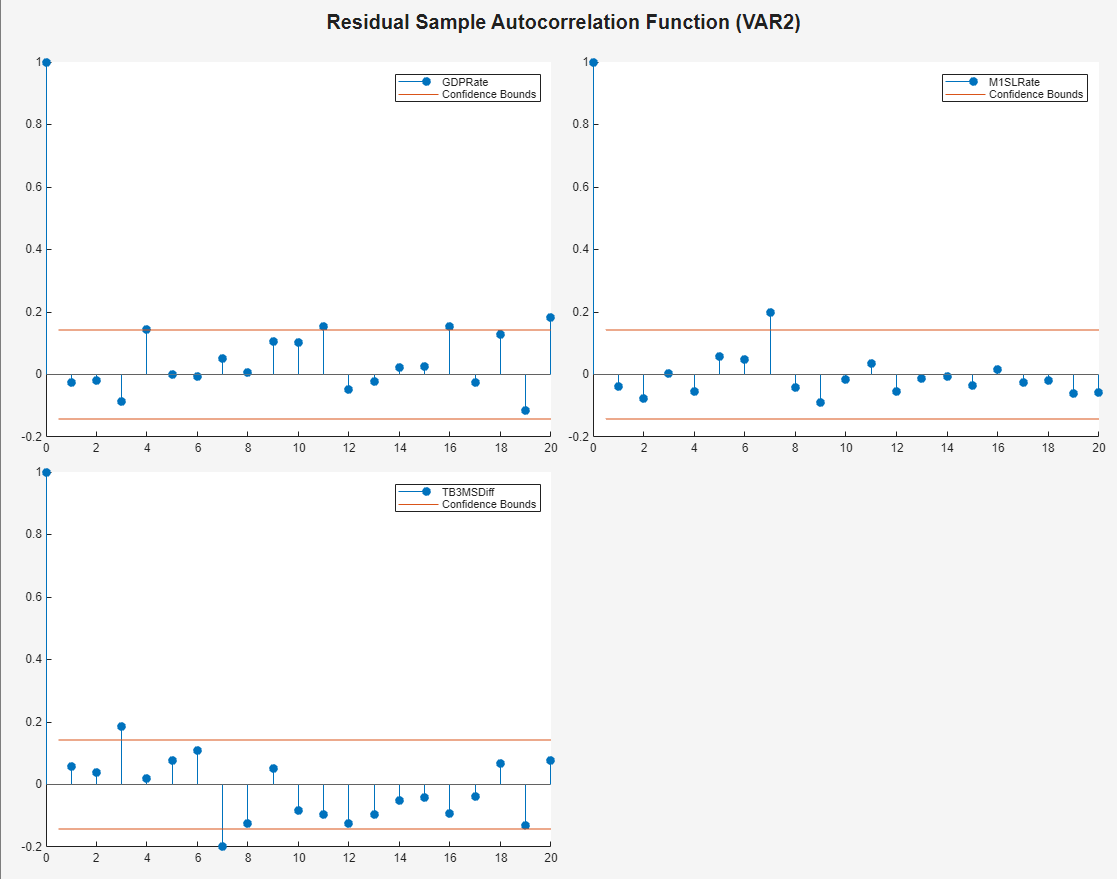
Each series has several significant, albeit small,
autocorrelations. For example, the GDPRate residual series
has significant autocorrelations at lags 4 and 16, and the
M1SLRate and TB3MSDiff quarterly
difference series both have significant autocorrelations at lags 7. To address
the autocorrelations, you can include higher AR lags in the VAR model for
estimation, but this example proceeds without addressing the autocorrelations
this way.
Plot separate ACF plots of each squared residual series. With
VAR2 selected in the Time
Series pane, on the Econometric Modeler
tab, in the Diagnostics section, click Residual
Diagnostics > Squared Residual
Autocorrelation. ACF plots of the each squared residual series
appear in the ACF(VAR2)2 document.

The M1SLRate and
TB3MSDiff series have significant autocorrelations, which
suggests that heteroscedasticity is present. This example proceeds without
addressing possible heteroscedasticity.
Export Model to Workspace
Export the model to the workspace.
With the
VAR2model selected in the Models pane, on the Econometric Modeler tab, in the Export section, click Export > Export Variables.In the Export Variables dialog box, select the Select check box for
GDPRate,M1SLRate, andTB3MSDiff.Click Export.
The variables GDPRate, M1SLRate,
TB3MSDiff, and VAR2 appear in the
workspace.
Conduct Causality Analysis at Command Line
Determine whether series in the system Granger-cause the other series by
conducting 1-step, leave-one-out Granger-causality tests. Pass the estimated
VAR(2) model to gctest.
gctest(VAR2)
H0 Decision Distribution Statistic PValue CriticalValue
_______________________________________________ __________________ ____________ _________ __________ _____________
"Exclude lagged M1SLRate in GDPRate equation" "Reject H0" "Chi2(2)" 8.3934 0.015045 5.9915
"Exclude lagged TB3MSDiff in GDPRate equation" "Reject H0" "Chi2(2)" 16.924 0.00021133 5.9915
"Exclude lagged GDPRate in M1SLRate equation" "Cannot reject H0" "Chi2(2)" 3.1528 0.20672 5.9915
"Exclude lagged TB3MSDiff in M1SLRate equation" "Reject H0" "Chi2(2)" 20.855 2.9608e-05 5.9915
"Exclude lagged GDPRate in TB3MSDiff equation" "Reject H0" "Chi2(2)" 20.565 3.4229e-05 5.9915
"Exclude lagged M1SLRate in TB3MSDiff equation" "Cannot reject H0" "Chi2(2)" 0.41428 0.81291 5.9915
The null hypothesis of the 1-step leave-one-out Granger-causality test is that a series does not 1-step Granger-cause another series, conditioned on all other series being present in the system. The results suggest:
Given that the 3-month T-bill change is in the system, enough evidence exists to suggest that M1 money supply rate 1-step Granger-causes the GDP rate.
Given that the M1 money supply rate is in the system, enough evidence exists to suggest that the 3-month T-bill change 1-step Granger-causes the GDP rate.
Given that the 3-month T-bill change is in the system, not enough evidence exists to suggest that the GDP rate 1-step Granger-causes the M1 money supply rate.
Given that the GDP rate is in the system, enough evidence exists to suggest that the 3-month T-bill change 1-step Granger-causes the M1 money supply rate.
Given that the M1 money supply rate is in the system, enough evidence exists to suggest that the GDP rate 1-step Granger-causes the 3-month T-bill change.
Given that the GDP rate is in the system, not enough evidence exists to suggest that the 1-step M1 money supply rate Granger-causes the 3-month T-bill change.
Generate Forecasts at Command Line
Generate forecasts and approximate 95% forecast intervals from the estimated
VAR(2) model for the next four years (16 quarters). For convenience, use the
entire series as a presample for the forecasts. The
forecast function discards all specified presample
observations except for the required final two
observations.
Y = [GDPRate M1SLRate TB3MSDiff]; [YF,YFMSE] = forecast(VAR2,16,Y); YFSE = cell2mat(cellfun(@(x)sqrt(diag(x)'),YFMSE, ... UniformOutput=false)); UB = YF + 1.96*YFSE; LB = YF - 1.96*YFSE; datesF = DataTimeTable.Time(end) + calquarters(1:16); figure tiledlayout(3,1) for j = 1:VAR2.NumSeries nexttile h1 = plot(DataTimeTable.Time(end-30:end),Y(end-30:end,j), ... Color=[.75,.75,.75]); hold on h2 = plot(datesF,YF(:,j),"r",LineWidth=2); h3 = plot(datesF,UB(:,j),"k--",LineWidth=1.5); plot(datesF,LB(:,j),"k--",LineWidth=1.5); ct = [Y(end,j) YF(1,j); Y(end,j) LB(1,j); Y(end,j) UB(1,j);]; plot([DataTimeTable.Time(end); datesF(1)],ct,Color=[.75,.75,.75]) legend([h1 h2 h3],VAR2.SeriesNames(j),"Forecast", ... "Forecast interval",Location="northwest") hold off end
