Gene Expression Analysis

The Problem: Analyzing Gene Expressions in Baker's Yeast (Saccharomyces Cerevisiae)

The goal is to gain some understanding of gene expressions in Saccharomyces cerevisiae, which is commonly known as baker's yeast or brewer's yeast. It is the fungus that is used to bake bread and ferment wine from grapes.

Saccharomyces cerevisiae, when introduced in a medium rich in glucose, can convert glucose to ethanol. Initially, yeast converts glucose to ethanol by a metabolic process called "fermentation". However, once the supply of glucose is exhausted yeast shifts from anaerobic fermentation of glucose to aerobic respiration of ethanol. This process is called diauxic shift. This process is of considerable interest since it is accompanied by major changes in gene expression.

The example uses DNA microarray data to study temporal gene expression of almost all genes in Saccharomyces cerevisiae during the diauxic shift.

You need Bioinformatics Toolbox™ to run this example.

if ~nnDependency.bioInfoAvailable
    errordlg('This example requires Bioinformatics Toolbox.');
    return;
end

The Data

This example uses data from DeRisi, JL, Iyer, VR, Brown, PO. "Exploring the metabolic and genetic control of gene expression on a genomic scale." Science. 1997 Oct 24;278(5338):680-6. PMID: 9381177

The full data set can be downloaded from the Gene Expression Omnibus website: https://www.yeastgenome.org

Start by loading the data into MATLAB®.

load yeastdata.mat

Gene expression levels were measured at seven time points during the diauxic shift. The variable times contains the times at which the expression levels were measured in the experiment. The variable genes contains the names of the genes whose expression levels were measured. The variable yeastvalues contains the "VALUE" data or LOG_RAT2N_MEAN, or log2 of ratio of CH2DN_MEAN and CH1DN_MEAN from the seven time steps in the experiment.

To get an idea of the size of the data you can use numel(genes) to show how many genes there are in the data set.

numel(genes)

genes is a cell array of the gene names. You can access the entries using MATLAB cell array indexing:

genes{15}

This indicates that the 15th row of the variable yeastvalues contains expression levels for the ORF YAL054C.

Filtering the Genes

The data set is quite large and a lot of the information corresponds to genes that do not show any interesting changes during the experiment. To make it easier to find the interesting genes, the first thing to do is to reduce the size of the data set by removing genes with expression profiles that do not show anything of interest. There are 6400 expression profiles. You can use a number of techniques to reduce this to some subset that contains the most significant genes.

If you look through the gene list you will see several spots marked as 'EMPTY'. These are empty spots on the array, and while they might have data associated with them, for the purposes of this example, you can consider these points to be noise. These points can be found using the strcmp function and removed from the data set with indexing commands.

emptySpots = strcmp('EMPTY',genes);
yeastvalues(emptySpots,:) = [];
genes(emptySpots) = [];
numel(genes)

In the yeastvalues data you will also see several places where the expression level is marked as NaN. This indicates that no data was collected for this spot at the particular time step. One approach to dealing with these missing values would be to impute them using the mean or median of data for the particular gene over time. This example uses a less rigorous approach of simply throwing away the data for any genes where one or more expression level was not measured.

The function isnan is used to identify the genes with missing data and indexing commands are used to remove the genes with missing data.

nanIndices = any(isnan(yeastvalues),2);
yeastvalues(nanIndices,:) = [];
genes(nanIndices) = [];
numel(genes)

If you were to plot the expression profiles of all the remaining profiles, you would see that most profiles are flat and not significantly different from the others. This flat data is obviously of use as it indicates that the genes associated with these profiles are not significantly affected by the diauxic shift; however, in this example, you are interested in the genes with large changes in expression accompanying the diauxic shift. You can use filtering functions in the Bioinformatics Toolbox™ to remove genes with various types of profiles that do not provide useful information about genes affected by the metabolic change.

You can use the genevarfilter function to filter out genes with small variance over time. The function returns a logical array of the same size as the variable genes with ones corresponding to rows of yeastvalues with variance greater than the 10th percentile and zeros corresponding to those below the threshold.

mask = genevarfilter(yeastvalues);
% Use the mask as an index into the values to remove the filtered genes.
yeastvalues = yeastvalues(mask,:);
genes = genes(mask);
numel(genes)

The function genelowvalfilter removes genes that have very low absolute expression values. Note that the gene filter functions can also automatically calculate the filtered data and names.

[mask, yeastvalues, genes] = ...
    genelowvalfilter(yeastvalues,genes,'absval',log2(3));
numel(genes)

Use geneentropyfilter to remove genes whose profiles have low entropy:

[mask, yeastvalues, genes] = ...
    geneentropyfilter(yeastvalues,genes,'prctile',15);
numel(genes)

Principal Component Analysis

Now that you have a manageable list of genes, you can look for relationships between the profiles.

Normalizing the standard deviation and mean of data allows the network to treat each input as equally important over its range of values.

Principal-component analysis (PCA) is a useful technique that can be used to reduce the dimensionality of large data sets, such as those from microarray analysis. This technique isolates the principal components of the dataset eliminating those components that contribute the least to the variation in the data set.

The two settings variables can be used to apply mapstd and processpca to new data to be consistent.

[x,std_settings] = mapstd(yeastvalues');  % Normalize data
[x,pca_settings] = processpca(x,0.15);    % PCA

The input vectors are first normalized, using mapstd, so that they have zero mean and unity variance. processpca is the function that implements the PCA algorithm. The second argument passed to processpca is 0.15. This means that processpca eliminates those principal components that contribute less than 15% to the total variation in the data set. The variable pc now contains the principal components of the yeastvalues data.

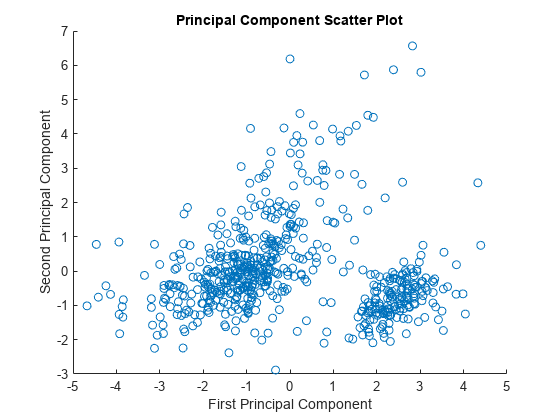
The principal components can be visualized using the scatter function.

figure
scatter(x(1,:),x(2,:));
xlabel('First Principal Component');
ylabel('Second Principal Component');
title('Principal Component Scatter Plot');

Cluster Analysis: Self-Organizing Maps

The principal components can now be clustered using the Self-Organizing map (SOM) clustering algorithm.

The selforgmap function creates a Self-Organizing map network which can then be trained with the train function.

The input size is 0 because the network has not yet been configured to match our input data. This will happen when the network is trained.

net = selforgmap([5 3]);
view(net)

Now the network is ready to be trained.

The Neural Network Training Tool shows the network being trained and the algorithms used to train it. It also displays the training state during training and the criteria which stopped training will be highlighted in green.

The buttons at the bottom open useful plots which can be opened during and after training. Links next to the algorithm names and plot buttons open documentation on those subjects.

net = train(net,x);

Use plotsompos to display the network over a scatter plot of the first two dimensions of the data.

figure
plotsompos(net,x);

You can assign clusters using the SOM by finding the nearest node to each point in the data set.

y = net(x);
cluster_indices = vec2ind(y);

Use plotsomhits to see how many vectors are assigned to each of the neurons in the map.

figure
plotsomhits(net,x);

You can also use other clustering algorithms like Hierarchical clustering and K-means, available in the Statistics and Machine Learning Toolbox™ for cluster analysis.

Glossary

ORF - An open reading frame (ORF) is a portion of a gene's sequence that contains a sequence of bases, uninterrupted by stop sequences, that could potentially encode a protein.