Fitting Values at N-D Grid with Tensor-Product Splines
Vector-valued splines are also used in the approximation to gridded data, in any number of variables, using tensor-product splines. The same spline-construction commands are used, only the form of the input differs. For example, if x is an m-vector, y is an n-vector, and z is an array of size [m,n], then cs = csapi({x,y},z); describes a bicubic spline f satisfying for . Such a multivariate spline can be vector-valued. For example, the following gives a perfectly acceptable sphere.
x = 0:4;
y = -2:2;
s2 = 1/sqrt(2);
z(3,:,:) = [0 1 s2 0 -s2 -1 0].'*[1 1 1 1 1];
z(2,:,:) = [1 0 s2 1 s2 0 -1].'*[0 1 0 -1 0];
z(1,:,:) = [1 0 s2 1 s2 0 -1].'*[1 0 -1 0 1];
sph = csape({x,y},z,["clamped","periodic"]);
fnplt(sph)
axis equal
axis off
title("Sphere Made by 3-D-Valued " + ...
"Bivariate Tensor Product Spline")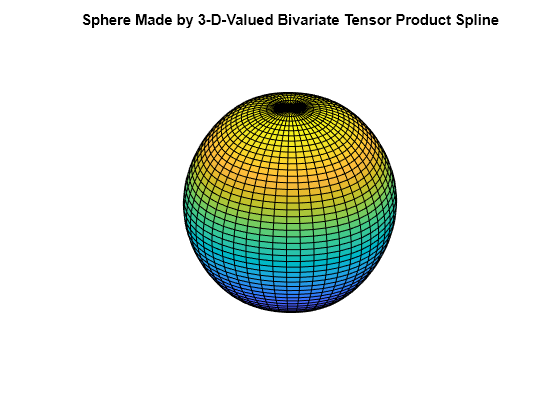
The sphere's projection onto the (x,z)-plane is plotted by the following.
fnplt(fncmb(sph,[1 0 0; 0 0 1])) axis equal axis off title("Planar Projection of Spline Sphere")
