Construct Chebyshev Spline

Chebyshev (a.k.a. Equioscillating) Spline Defined

By definition, for given knot sequence t of length n+k, C = C_{t,k} is the unique element of S_{t,k} of max-norm 1 that maximally oscillates on the interval [t_k .. t_{n+1}] and is positive near t_{n+1}. This means that there is a unique strictly increasing tau of length n so that the function C in S_{k,t} given by

C(tau(i)) = (-1)^{n-i},

for all i, has max-norm 1 on [t_k .. t_{n+1}]. This implies that

tau(1) = t_k,

tau(n) = t_{n+1},

and that

t_i < tau(i) < t_{k+i},

for all i. In fact,

t_{i+1} <= tau(i) <= t_{i+k-1},

for all i. This brings up the point that the knot sequence t is assumed to make such an inequality possible, which turns out to be equivalent to having all the elements of S_{k,t} continuous.

t = augknt([0 1 1.1 3 5 5.5 7 7.1 7.2 8], 4 );
[tau,C] = chbpnt(t,4);
xx = sort([linspace(0,8,201),tau]);
plot(xx,fnval(C,xx),'LineWidth',2);
hold on
breaks = knt2brk(t); 
bbb = repmat(breaks,3,1);
sss = repmat([1;-1;NaN],1,length(breaks));
plot(bbb(:), sss(:),'r');
hold off
ylim([-2 2]);
title('The Chebyshev Spline for a Particular Knot Sequence');
legend({'Chebyshev Spline' 'Knots'});

In short, the Chebyshev spline C looks just like the Chebyshev polynomial. It performs similar functions. For example, its extrema tau are particularly good sites to interpolate at from S_{k,t} since the norm of the resulting projector is about as small as can be.

hold on
plot(tau,zeros(size(tau)),'k+');
hold off
legend({'Chebyshev Spline' 'Knots' 'Extrema'});

Choice of Spline Space

In this example, we try to construct C for a given spline space.

We deal with cubic splines with simple interior knots, specified by

k = 4;
breaks = [0 1 1.1 3 5 5.5 7 7.1 7.2 8];
t = augknt(breaks, k)

t = 1×16

         0         0         0         0    1.0000    1.1000    3.0000    5.0000    5.5000    7.0000    7.1000    7.2000    8.0000    8.0000    8.0000    8.0000

thus getting a spline space of dimension

n = length(t)-k

n = 
12

Initial Guess

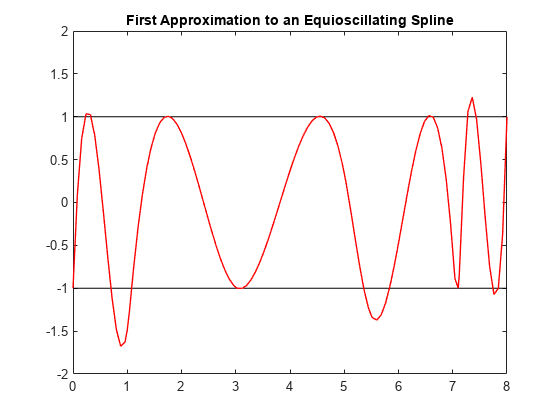
As our initial guess for the tau, we use the knot averages

tau(i) = (t_{i+1} + ... + t_{i+k-1})/(k-1)

recommended as good interpolation site choices, and plot the resulting first approximation to C.

tau = aveknt(t,k)

tau = 1×12

         0    0.3333    0.7000    1.7000    3.0333    4.5000    5.8333    6.5333    7.1000    7.4333    7.7333    8.0000

b = (-ones(1,n)).^(n-1:-1:0);
c = spapi(t,tau,b);
plot(breaks([1 end]),[1 1],'k', breaks([1 end]),[-1 -1],'k');
hold on
fnplt(c,'r',1);
hold off
ylim([-2 2]);
title('First Approximation to an Equioscillating Spline');

Iteration

For the complete leveling, use the Remez algorithm. This means that we construct a new tau as the extrema of our current approximation, c, to C and try again.

To find the extrema, first calculate the derivative Dc of the current approximation c.

Dc = fnder(c);

Take the zeros of Dc using the fnzeros function.The zeros represent the extrema of the current approximation c. The result is the new guess for tau.

tau(2:n-1) = mean(fnzeros(Dc))

tau = 1×12

         0    0.2765    0.9057    1.7438    3.0779    4.5531    5.5830    6.5841    7.0809    7.3464    7.7889    8.0000

plot(breaks([1 end]),[1 1],'k', breaks([1 end]),[-1 -1],'k');
hold on
fnplt(c,'r',1);
plot(tau(2:n-1),zeros(1,n-2),'x');
hold off
title('First Approximation to an Equioscillating Spline');
ax = gca;
h = ax.Children;
legend(h([2 1]),{'Approximation','Extrema'});
axis([0 8 -2 2]);

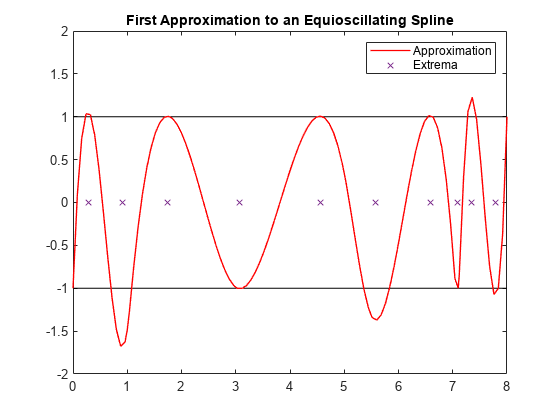
End of First Iteration Step

We compute the resulting new approximation to the Chebyshev spline using the new guess for tau.

cnew = spapi(t,tau,b);

The new approximation is more nearly an equioscillating spline.

plot(breaks([1 end]),[1 1],'k', breaks([1 end]),[-1 -1],'k');
hold on
fnplt(c,'r',1);
fnplt(cnew, 'k', 1);
hold off
ax = gca;
h = ax.Children;
legend(h([2 1]),{'First Approximation' 'Updated Approximation'});
axis([0 8 -2 2]);

If this is not close enough, simply try again, starting from this new tau. For this particular example, the next iteration already provides the Chebyshev spline to graphic accuracy.

Use of Chebyshev-Demko Points

The Chebyshev spline for a given spline space S_{k,t}, along with its extrema, are available as optional outputs from the chbpnt command in the toolbox. These extrema were proposed as good interpolation sites by Steven Demko, hence are now called the Chebyshev-Demko sites. This section shows an example of their use.

If you have decided to approximate the square-root function on the interval [0 .. 1] by cubic splines with knot sequence

k = 4;
n = 10;
t = augknt(((0:n)/n).^8,k);

then a good approximation to the square-root function from that specific spline space is given by

tau = chbpnt(t,k);
sp = spapi(t,tau,sqrt(tau));

as is evidenced by the near equioscillation of the error.

xx = linspace(0,1,301);
plot(xx, fnval(sp,xx)-sqrt(xx));
title({'Error in Interpolant to Square Root','at Chebyshev-Demko Sites.'});