comm.PAMDemodulator
(Not recommended) Demodulate using M-ary pulse amplitude demodulation
comm.PAMDemodulator is not recommended. Use pamdemod instead. For more information, see Version History.
Description
The comm.PAMDemodulator
System object™ demodulates a signal that was
modulated using M-ary pulse amplitude modulation (M-PAM)
method. The input is a baseband representation of the modulated signal.
To demodulate a signal that was modulated using M-PAM method:
Create the
comm.PAMDemodulatorobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
pamdemodulator = comm.PAMDemodulator
pamdemodulator = comm.PAMDemodulator(Name=Value)ModulationOrder=2 sets the number of points in the signal
constellation to 2.
pamdemodulator = comm.PAMDemodulator(M,Name=Value)ModulationOrder property by
using M input
argument.
Input Arguments
Modulation order, specified as an positive even integer. M
represents the number of points in signal constellation.
Data Types: double
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
General Properties
Number of points in the signal constellation, specified as one of these options.
The comm.PAMDemodulatorSystem object scales the signal constellation based on how you set the NormalizationMethod
property.
Bit output, specified as a numeric or logical 0
(false) or 1 (true).
1(true) — Use this option to set the object output,Y, to a column vector of bit values that represents integers. The binary-valued signals are grouped in K = log2(M) bits, where K is the number of bits per symbol and M is the modulation order. The output vector length must be an integer multiple of K.0(false) — Use this option to set the object output,Y, to a column vector with length equal to the input vector,X. This value contains integer symbol values in the range [0, M - 1]. M is the modulation order.
Data Types: logical
Constellation encoding, specified as "Gray" or
"Binary".
Symbol mapping specifies how the object maps an integer or group of log2(ModulationOrder) input bits to the corresponding symbol.
When you set this property to
"Gray", the object uses a Gray-encoded signal constellation.When you set this property to
"Binary", the input integer m maps to the complex value 2m – M + 1. M is the property ModulationOrder value and m lies in the range [0, (M – 1)].
Constellation normalization method used to normalize the signal constellation,
specified as "Minimum distance between symbols", "Average
power", or "Peak power".
Minimum distance between two symbols, specified as a positive scalar.
Dependencies
To enable this property, set the NormalizationMethod
property is set to "Minimum distance between symbols".
Data Types: double
Average power of the symbols in the constellation, specified as a positive scalar.
Dependencies
To enable this property, set the NormalizationMethod
property is set to "Average power".
Data Types: double
Peak power of the symbols in the constellation, specified as a positive scalar.
Dependencies
To enable this property, set the NormalizationMethod
property is set to "Peak power".
Data Types: double
Data type of output, specified as either "Full precision",
"Smallest unsigned integer", "double",
"single", "int8", "uint8",
"int16", "uint16", "int32",
"uint32", or "logical".
When you set this property to
"Full precision", and the input data type is single or double precision, the output data has the same data type as that of the input.When the input signal is an integer data type, you must have a Fixed-Point Designer™ user license to use this property in
"Smallest unsigned integer"or"Full precision"mode.When the input data is of a fixed-point type, the output data type behaves as if you had set the
OutputDataTypeproperty to"Smallest unsigned integer".When you set the BitOutput property to
true, then"logical"data type becomes a valid option.
Fixed-Point Properties
Full precision override for fixed-point arithmetic, specified as a numeric or
logical 0 (false) or 1
(true).
When you set this property to
true, the object computes all internal arithmetic and output data types using full precision rules. These rules provide the most accurate fixed-point numerics. It also turns off the display of other fixed-point properties because they do not apply individually. These rules guarantee that no quantization occurs within the object. Bits are added, as needed, to ensure that no roundoff or overflow occurs.When you set this property to
false, fixed-point data types are controlled through individual fixed-point property settings.
For more information, see Full Precision for Fixed-Point System Objects.
Data Types: logical
Data type of denormalization factor, specified as "Same word length as
input" or "Custom".
Fixed-point data type of denormalization factor, specified as an unscaled
numerictype (Fixed-Point Designer) function with the
Signedness name-value argument set to
"Auto".
Dependencies
To enable this property, set the DenormalizationFactorDataType property to
"Custom".
Product data type, specified as "Full precision" or
"Custom". When you set this property to "Full
precision" the comm.PAMDemodulator calculates the full-precision
product word and fraction lengths.
Dependencies
To enable this property, set the FullPrecisionOverride property to false.
Fixed-point data type of the product, specified as an unscaled numerictype (Fixed-Point Designer) function with the Signedness name-value
argument set to "Auto".
Dependencies
To enable this property, set the FullPrecisionOverride property to false and the
ProductDataType
property to "Custom".
Rounding of fixed-point numeric value of the product, specified as either
"Ceiling", "Convergent",
"Floor", "Nearest",
"Round", "Simplest", or
"Zero".
This property applies when the object is not in a full precision configuration
Product overflow action when fixed-point numeric value of product overflows,
specified as "Wrap" or "Saturate".
This property applies when the object is not in a full precision configuration.
Data type of sum, specified as one either "Full precision",
"Same as product", or "Custom". When you set
this property to "Full precision", the object calculates the
full-precision sum word and fraction lengths.
Dependencies
To enable this property, set the FullPrecisionOverride property to false.
Fixed-point data type of sum, specified as an unscaled numerictype (Fixed-Point Designer) function with the Signedness name-value
argument set to "Auto".
Dependencies
To enable this property, set the FullPrecisionOverride property to false and
SumDataType property to
"Custom".
Usage
Description
Input Arguments
M-PAM modulated baseband signal, specified as a scalar or column vector.
Data Types: single | double | int8 | int16 | int32 | int64 | signed fi
Complex Number Support: Yes
Output Arguments
Demodulated data, returned as a scalar or column vector.
Depending on the BitOutput property value,
Y can be integer or bit-valued. The dimensions of the
demodulated signal depend on the value that you specify for the OutputDataType
property.
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
constellation | Calculate or plot ideal signal constellation |
Examples
Modulate and demodulate a signal using 16-PAM modulation.
hMod = comm.PAMModulator(16); hAWGN = comm.AWGNChannel("NoiseMethod", ... "Signal to noise ratio (SNR)", ... SNR=20, SignalPower=85); hDemod = comm.PAMDemodulator(16); % Create an error rate calculator hError = comm.ErrorRate; for counter = 1:100 % Transmit a 50-symbol frame data = randi([0 hMod.ModulationOrder-1],50,1); modSignal = hMod(data); noisySignal = hAWGN(modSignal); receivedData = hDemod(noisySignal); errorStats = hError(data,receivedData); end fprintf('Error rate = %f\nNumber of errors = %d\n', ... errorStats(1), errorStats(2))
Error rate = 0.112600 Number of errors = 563
Algorithms
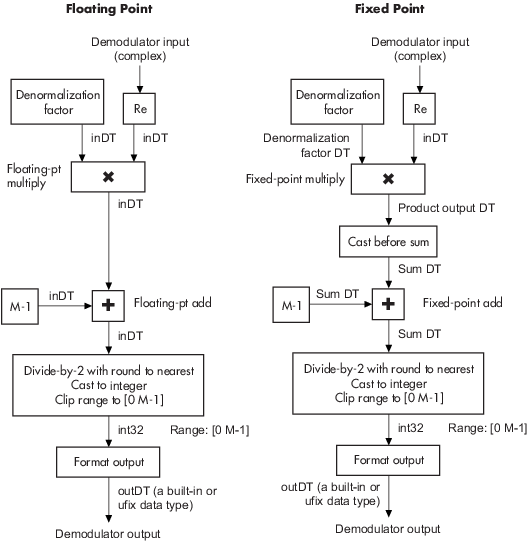
The demodulator algorithm maps received input signal constellation values to M-ary integer symbol indices in the range [0, M – 1], and then maps these demodulated symbol indices to formatted output values.
The demodulator computes the integer symbol index by first scaling the real part of the received input signal by a denormalization factor derived from the normalization method and related parameters.
To translate the received signal into the approximate range of [0, 2(M – 1)] plus noise, add the denormalized value to (M – 1).
To obtain a range approximately between [0, M – 1] plus noise, rescale the resulting value via a divide-by-two (or, equivalently, a right-shift by one bit for fixed-point operation).
Round the noisy index value to the nearest integer and clip, via saturation, to the exact range of [0 M – 1].
Finally, based on other block parameters, map the integer index to a symbol value that is formatted and cast to the selected output data type.
These figures contain side-by-side signal flow diagrams for floating-point and fixed-point algorithm operation.
The floating-point diagrams apply when the input signal data type is
doubleorsingle.The fixed-point diagrams apply when the input signal is a signed fixed-point data type.
Separate signal flows are shown for denormalization factor set to unity or nonunity. Setting the denormalization factor to 1, normalizes the constellation and simplifies the signal flow.
This figure shows the floating-point and fixed-point demodulation signal-flow diagram with unity denormalization factor.

This figure shows the floating-point and fixed-point demodulation signal-flow diagram with nonunity denormalization factor.
FullPrecisionOverride is a convenience property that,
when you set it to true, automatically sets the appropriate properties
for an object to use full-precision to process fixed-point input.
For System objects, full precision, fixed-point operation refers to growing just enough
additional bits to compute the ideal full-precision result. This operation has no minimum or
maximum range overflow nor any precision loss due to rounding or underflow. It is also
independent of any hardware-specific settings. The data types chosen are based only on known
data type ranges and not on actual numeric values. Full-precision for System objects does
not optimize coefficient values. When you set the FullPrecisionOverride
property to true, the other fixed-point properties it controls no longer
apply and any of their nondefault values are ignored. These properties are also hidden. To
specify individual fixed-point properties, first set
FullPrecisionOverride to false.
Extended Capabilities
Usage notes and limitations:
See System Objects in MATLAB Code Generation (MATLAB Coder).
Version History
Introduced in R2012acomm.PAMDEmodulator is not recommended. Use pamdemod
instead.
n = 10000; % Number of symbols to process M = 8; % Modulation order x = randi([0 M-1],n,1); % Create message signal %% Using PAM modulation and demodulation system objects pammodObj = comm.PAMModulator(M); pamdemodObj = comm.PAMDemodulator(M); yOld = pammodObj(x); % Modulate % ... channel filtering ... zOld = pamdemodObj(complex(yOld)); % Demodulate %% Using PAM modulation and demodulation functions yNew = pammod(x,M); % Modulate % ... channel filtering ... zNew = pamdemod(y,M); % Demodulate isequal(zOld,zNew)
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Website auswählen
Wählen Sie eine Website aus, um übersetzte Inhalte (sofern verfügbar) sowie lokale Veranstaltungen und Angebote anzuzeigen. Auf der Grundlage Ihres Standorts empfehlen wir Ihnen die folgende Auswahl: .
Sie können auch eine Website aus der folgenden Liste auswählen:
So erhalten Sie die bestmögliche Leistung auf der Website
Wählen Sie für die bestmögliche Website-Leistung die Website für China (auf Chinesisch oder Englisch). Andere landesspezifische Websites von MathWorks sind für Besuche von Ihrem Standort aus nicht optimiert.
Amerika
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)