Generate Generic C Code for Sequence-to-Sequence Regression Using Deep Learning
This example demonstrates how to generate plain C code that does not depend on any third-party deep learning libraries for a long short-term memory (LSTM) network. You generate a MEX function that accepts time series data representing various sensors in an engine. The MEX function then makes predictions for each step of the input time series to predict the remaining useful life (RUL) of the engine measured in cycles.
This example uses the Turbofan Engine Degradation Simulation data set from [1] and a pretrained LSTM network. The network was trained on simulated time series sequence data for 100 engines and the corresponding values of the remaining useful life at the end of each sequence. Each sequence in this training data has a different length and corresponds to a full run to failure (RTF) instance. For more information on training the network, see the example Sequence-to-Sequence Regression Using Deep Learning (Deep Learning Toolbox).
The rulPredict Entry-Point Function
The rulPredict entry-point function takes an input sequence and passes it to a trained sequence-to-sequence LSTM network for prediction. The function loads the network object from the rulDlnetwork.mat file into a persistent variable and reuses the persistent object on subsequent prediction calls. The LSTM network makes predictions on the partial sequence one time step at a time. At each time step, the network predicts using the value at this time step, and the network state calculated from the previous time steps. The network updates its state between each prediction. The predict function returns a sequence of these predictions. The last element of the prediction corresponds to the predicted RUL for the partial sequence.
To display an interactive visualization of the network architecture and information about the network layers, use the analyzeNetwork (Deep Learning Toolbox) function.
type rulPredict.mfunction out = rulPredict(in, dataFormat)
%#codegen
% Copyright 2020-2023 The MathWorks, Inc.
persistent mynet;
if isempty(mynet)
mynet = coder.loadDeepLearningNetwork('rulDlnetwork.mat');
end
% Construct formatted dlarray input
dlIn = dlarray(in, dataFormat);
dlOut = predict(mynet, dlIn);
out = extractdata(dlOut);
end
Download and Prepare Test Data
First, download and prepare the test data for the example. For more information on the Turbofan Engine Degradation Simulation data set and the preprocessing steps, see the example Sequence-to-Sequence Regression Using Deep Learning (Deep Learning Toolbox).
Download Data Set
Create a directory and then download and extract the Turbofan Engine Degradation Simulation data set.
dataFolder = fullfile(tempdir,"turbofan"); if ~isfolder(dataFolder) mkdir(dataFolder); end filename = matlab.internal.examples.downloadSupportFile("nnet","data/TurbofanEngineDegradationSimulationData.zip"); unzip(filename,dataFolder)
Calculate Mean and Standard Deviation of Training Data
Calculate the normalization parameters for the training data. These parameters are required to normalize the test predictors using the mean and standard deviation of the training data.
Load the training data. Each column is one observation and each row is one feature. Remove the features that have constant values.
filenamePredictors = fullfile(dataFolder,"train_FD001.txt"); [XTrain] = processTurboFanDataTrain(filenamePredictors); m = min([XTrain{:}],[],2); M = max([XTrain{:}],[],2); idxConstant = M == m; for i = 1:numel(XTrain) XTrain{i}(idxConstant,:) = []; end
Calculate the mean and standard deviation over all observations.
mu = mean([XTrain{:}],2);
sig = std([XTrain{:}],0,2);Prepare Test Data
Prepare the test data using the function processTurboFanDataTest. The function extracts the data from filenamePredictors and filenameResponses and returns the cell arrays XValidate and YValidate, which contain the test predictor and response sequences, respectively.
filenamePredictors = fullfile(dataFolder,"test_FD001.txt"); filenameResponses = fullfile(dataFolder,"RUL_FD001.txt"); [XValidate,YValidate] = processTurboFanDataTest(filenamePredictors,filenameResponses);
Remove the features with constant values by using the idxConstant that you calculated from the training data. Normalize the test predictors using the parameters mu and sig that you calculated from the training data. Clip the test responses at the threshold of 150, which is the same threshold value used to train the network.
thr = 150; for i = 1:numel(XValidate) XValidate{i}(idxConstant,:) = []; XValidate{i} = (XValidate{i} - mu) ./ sig; YValidate{i}(YValidate{i} > thr) = thr; end
The entry-point function rulPredict requires a data format to construct a dlarray input to the dlnetwork. The first dimension of the dlarray object is channel 'C' and the second dimension is the sequence length 'T'. Finally, cast the data to single for deployment.
dataFormat = 'CT'; XValidate = cellfun(@single, XValidate, 'UniformOutput', false); YValidate = cellfun(@single, YValidate, 'UniformOutput', false);
Run rulPredict on Test Data
The variable XValidate contains sample time series data for the sensor readings that you use to test the entry-point function in MATLAB®. Make predictions on the test data by calling the rulPredict method.
numValidateElements = numel(XValidate); YPred = cell(numValidateElements, 1); for i = 1:numValidateElements YPred{i} = rulPredict(XValidate{i}, dataFormat); end
Visualize some of the predictions in a plot.
idx = randperm(numel(YPred),4); figure for i = 1:numel(idx) subplot(2,2,i) plot(YValidate{idx(i)},'--') hold on plot(YPred{idx(i)},'.-') hold off ylim([0 175]) title("Test Observation " + idx(i)) xlabel("Time Step") ylabel("RUL") end

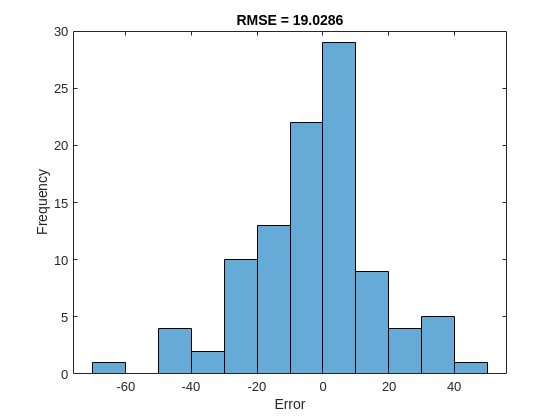
For a given partial sequence, the predicted current RUL is the last element of the predicted sequences. Calculate the root-mean-square error (RMSE) of the predictions, and visualize the prediction error in a histogram.
YValidateLast = zeros(1, numel(YValidate)); YPredLast = zeros(1, numel(YValidate)); for i = 1:numel(YValidate) YValidateLast(i) = YValidate{i}(end); YPredLast(i) = YPred{i}(end); end figure rmse = sqrt(mean((YPredLast - YValidateLast).^2))
rmse = 19.0286
histogram(YPredLast - YValidateLast) title("RMSE = " + rmse) ylabel("Frequency") xlabel("Error")
Generate MEX Function for the rulPredict Entry-Point Function
To generate a MEX function for the rulPredict entry-point function, create a code generation configuration object, cfg, for MEX code generation. Create a deep learning configuration object that specifies no deep learning library is required and attach this deep learning configuration object to cfg.
cfg = coder.config('mex'); cfg.DeepLearningConfig = coder.DeepLearningConfig('TargetLibrary','none');
Use the coder.typeof function to create the input type for the entry-point function rulPredict that you use with the -args option in the codegen command.
The XValidate variable contains 100 observations, and each observation is of single data type and has a feature dimension value of 17 and a variable sequence length. Each observation must have the same feature dimension, but the sequence lengths can vary. To perform prediction on a sequence of any length, specify the sequence length as variable-size enables us. We can do this by setting the sequence length size to Inf and the variable size to true in coder.typeof.
arrayInput = coder.typeof(single(0), [17 Inf],[false true]);
Run the codegen command. Specify the input type as arrayInput.
codegen('rulPredict','-config', cfg, '-args', {arrayInput, coder.Constant(dataFormat)});
Code generation successful.
Run Generated MEX Function on Test Data
Make predictions on the test data by calling the generated MEX function rulPredict_mex.
YPredMex = cell(numValidateElements, 1); for i = 1:numValidateElements YPredMex{i} = rulPredict_mex(XValidate{i}, dataFormat); end
You can visualize the predictions in a plot.
figure for i = 1:numel(idx) subplot(2,2,i) plot(YValidate{idx(i)},'--') hold on plot(YPredMex{idx(i)},'.-') hold off ylim([0 175]) title("Test Observation " + idx(i)) xlabel("Time Step") ylabel("RUL") end legend(["Test Data" "Predicted MEX"],'Location','southeast')

Calculate the root-mean-square error (RMSE) of the predictions and visualize the prediction error in a histogram.
YPredLastMex = zeros(1, numel(YValidate)); for i = 1:numel(YValidate) YPredLastMex(i) = YPredMex{i}(end); end figure rmse = sqrt(mean((YPredLastMex - YValidateLast).^2))
rmse = 19.0286
histogram(YPredLastMex - YValidateLast) title("RMSE = " + rmse) ylabel("Frequency") xlabel("Error")

Generate MEX Function with Stateful LSTM
Instead of passing all of the time series data to the network to predict in one step, you can make predictions one time step at a time by updating the state of the dlnetwork. Making predictions one time step at a time is useful when the value of the time steps arrives in a stream. You can use the syntax [out, updatedState] = predict(net, in) to produce the output prediction and the updated network state. Then, you can assign the updated state to the network by using net.State = updatedState to update the internal state.
The entry-point function rulPredictAndUpdate takes a single-timestep input, updates the state of the network, and treats subsequent inputs as subsequent timesteps of the same sample. After passing in all timesteps one at a time, the resulting output is the same as if all timesteps were passed in as a single input.
type rulPredictAndUpdate.mfunction out = rulPredictAndUpdate(in, dataFormat)
%#codegen
% Copyright 2020-2023 The MathWorks, Inc.
persistent mynet;
if isempty(mynet)
mynet = coder.loadDeepLearningNetwork('rulDlnetwork.mat');
end
% Construct formatted dlarray input
dlIn = dlarray(in, dataFormat);
% Predict and update the state of the network
[dlOut, updatedState] = predict(mynet, dlIn);
mynet.State = updatedState;
out = extractdata(dlOut);
end
Run codegen on the new entry-point function. Because the function takes a single timestep each call, we specify that arrayInput has a fixed-sequence dimension of 1.
arrayInput = coder.typeof(single(0),[17 1]); codegen('rulPredictAndUpdate', '-config', cfg, '-args', {arrayInput, coder.Constant(dataFormat)});
Code generation successful.
Make predictions on the test data by calling the generated MEX function rulPredictAndUpdate_mex.
sampleIdx = idx(1);
sample = XValidate{sampleIdx};
numTimeStepsTest = size(sample, 2);
YPredStatefulMex = dlarray(zeros(size(YValidate{sampleIdx}), 'single'));
for iStep = 1:numTimeStepsTest
YPredStatefulMex(1, iStep) = rulPredictAndUpdate_mex(sample(:, iStep), dataFormat);
endFinally, you can visualize the results for the two different MEX functions and the MATLAB prediction in a plot for any particular sample.
figure()
plot(YValidate{sampleIdx},'--')
hold on
plot(YPred{sampleIdx},'o-')
plot(YPredMex{sampleIdx},'^-')
plot(YPredStatefulMex,'x-')
hold off
ylim([0 175])
title("Test Observation " + sampleIdx)
xlabel("Time Step")
ylabel("RUL")
legend(["Test Data" "Predicted in MATLAB" "Predicted MEX" "Predicted MEX with Stateful LSTM"],'Location','southeast')
References
Saxena, Abhinav, Kai Goebel, Don Simon, and Neil Eklund. "Damage propagation modeling for aircraft engine run-to-failure simulation." In Prognostics and Health Management, 2008. PHM 2008. International Conference on, pp. 1-9. IEEE, 2008.
See Also
coder.DeepLearningConfig | codegen | coder.config