Confidence Intervals for Sample Autocorrelation
This example shows how to create confidence intervals for the autocorrelation sequence of a white noise process. Create a realization of a white noise process with length samples. Compute the sample autocorrelation to lag 20. Plot the sample autocorrelation along with the approximate 95%-confidence intervals for a white noise process.
Create the white noise random vector. Set the random number generator to the default settings for reproducible results. Obtain the normalized sampled autocorrelation to lag 20.
rng default L = 1000; x = randn(L,1); [xc,lags] = xcorr(x,20,'coeff');
Create the lower and upper 95% confidence bounds for the normal distribution , whose standard deviation is . For a 95%-confidence interval, the critical value is and the confidence interval is
vcrit = sqrt(2)*erfinv(0.95)
vcrit = 1.9600
lconf = -vcrit/sqrt(L); upconf = vcrit/sqrt(L);
Plot the sample autocorrelation along with the 95%-confidence interval.
stem(lags,xc,'filled') hold on plot(lags,[lconf;upconf]*ones(size(lags)),'r') hold off ylim([lconf-0.03 1.05]) title('Sample Autocorrelation with 95% Confidence Intervals')
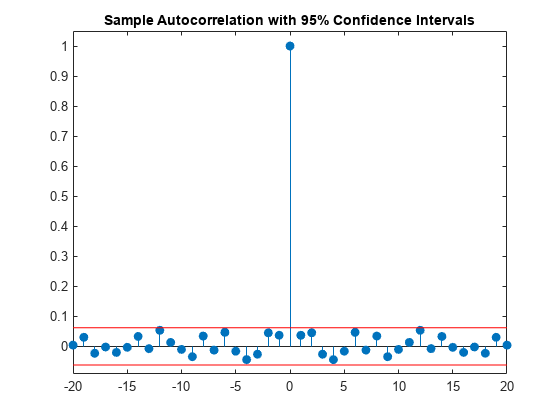
You see in the above figure that the only autocorrelation value outside of the 95%-confidence interval occurs at lag 0 as expected for a white noise process. Based on this result, you can conclude that the data are a realization of a white noise process.
