nuttallwin
Nuttall-defined minimum 4-term Blackman-Harris window
Description
w = nuttallwin(L)L-point, four-term symmetric
Blackman-Harris window. The coefficients for this window differ from the
Blackman-Harris window coefficients computed with blackmanharris and produce slightly
lower sidelobes.
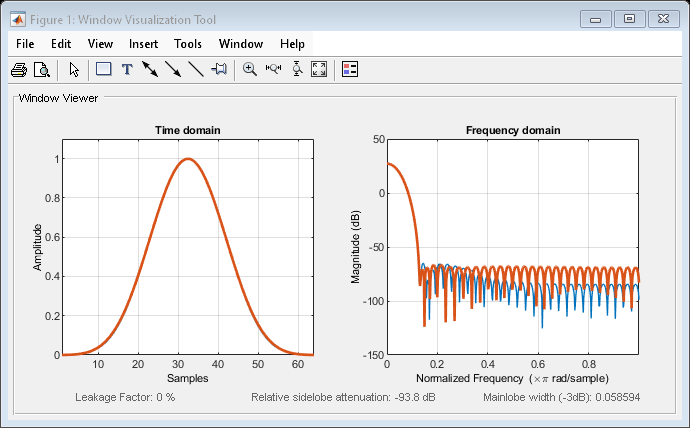
Examples
Input Arguments
Output Arguments
Algorithms
The equation for the symmetric Nuttall defined four-term Blackman-Harris window is
where n= 0,1,2, ... N-1.
The equation for the periodic Nuttall defined four-term Blackman-Harris window is
where n= 0,1,2, ... N-1. The periodic window is N-periodic.
The coefficients for this window are
a0 = 0.3635819
a1 = 0.4891775
a2 = 0.1365995
a3 = 0.0106411
References
[1] Nuttall, Albert H. “Some Windows with Very Good Sidelobe Behavior.” IEEE® Transactions on Acoustics, Speech, and Signal Processing. Vol. ASSP-29, February 1981, pp. 84–91.
Extended Capabilities
Version History
Introduced before R2006a
See Also
Apps
Functions
barthannwin|bartlett|blackmanharris|bohmanwin|parzenwin|rectwin|triang| WVTool