Shape of the Earth
Although the Earth is very round, it is an oblate spheroid rather than a perfect sphere. This difference is so small (only one part in 300) that modeling the Earth as spherical is sufficient for making small-scale (world or continental) maps. However, making accurate maps at larger scale demands that a spheroidal model be used. Such models are essential, for example, when you are mapping high-resolution satellite or aerial imagery, or when you are working with coordinates from the Global Positioning System (GPS). This section addresses how Mapping Toolbox™ software accurately models the shape, or figure, of the Earth.
Ellipsoid Shape
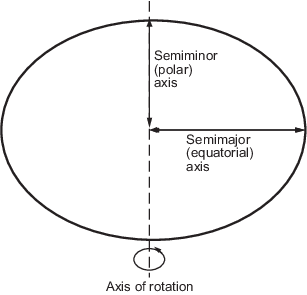
You can define ellipsoids in several ways. They are usually specified by a semimajor and a semiminor axis, but are often expressed in terms of a semimajor axis and either inverse flattening (which for the Earth, as mentioned above, is one part in 300) or eccentricity. Whichever parameters are used, as long as an axis length is included, the ellipsoid is fully constrained and the other parameters are derivable. The components of an ellipsoid are shown in the following diagram.
The toolbox includes ellipsoid models that represent the figures of the Sun, Moon, and planets, as well as a set of the most common ellipsoid models of the Earth. For more information, see Comparison of Reference Spheroids.
Geoid Shape
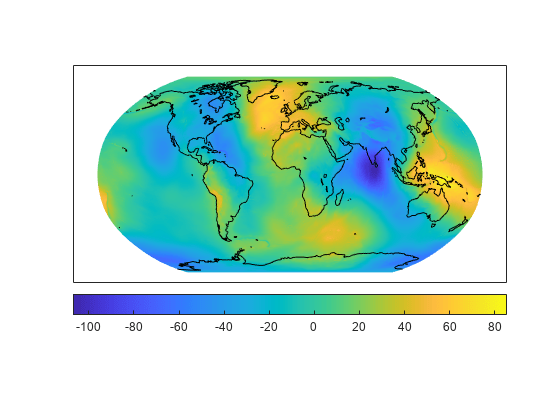
Literally, geoid means Earth-shaped. The geoid is an empirical approximation of the figure of the Earth (minus topographic relief), its "lumpiness." Specifically, it is an equipotential surface with respect to gravity, more or less corresponding to mean sea level. It is approximately an ellipsoid, but not exactly so because local variations in gravity create minor hills and dales (which range from -100 m to +60 m across the Earth). This variation in height is on the order of 1 percent of the differences between the semimajor and semiminor ellipsoid axes used to approximate the Earth's shape.
The shape of the geoid is important for some purposes, such as calculating satellite orbits, but need not be taken into account for every mapping application. However, knowledge of the geoid is sometimes necessary, for example, when you compare elevations given as height above mean sea level to elevations derived from GPS measurements. Geoid representations are also inherent in datum definitions.
Map the Geoid
Get geoid heights and a geographic postings reference object from the EGM96 geoid model. Load coastline latitude and longitude data.
[N,R] = egm96geoid;
load coastlinesDisplay the geoid heights as a surface using a Robinson projection. Ensure the coastline data appears over the surface by setting the 'CData' name-value pair to the geoid heights data and the 'ZData' name-value pair to a matrix of zeros. Then, display the coastline data.
axesm robinson Z = zeros(R.RasterSize); geoshow(N,R,'DisplayType','surface','CData',N,'ZData',Z) geoshow(coastlat,coastlon,'color','k')
Display a colorbar below the map.
colorbar('southoutside')