Interpret SimEvents Models Using Statistical Analysis
Choosing the right statistical measure is critical for evaluating the model performance. You can use output statistics from the SimEvents® library blocks for data analysis and run-time control.
Output Statistics for Data Analysis
Consider these statistical measures for more efficient behavior interpretation.
Identify the appropriate size of the samples to compute more meaningful statistics.
Decide if you want to investigate the transient behavior, the steady-state behavior, or both.
Specify the number of simulations that ensures sufficient confidence in the results.
For an example, see Explore Statistics and Visualize Simulation Results.
Output Statistics for Run-Time Control
Some systems rely on statistics to influence the dynamics. In this example, a queuing system with discouraged arrivals has a feedback loop that adjusts the arrival rate throughout the simulation based on the statistics reported by the queue and the server. To learn more details about this example, see Adjust Entity Generation Times Through Feedback.
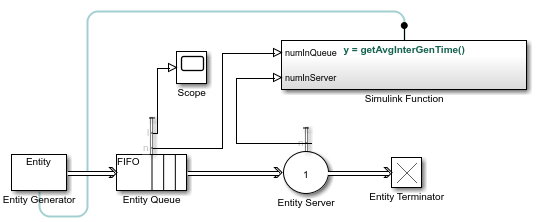
A subset of the blocks in SimEvents library provides statistics output for run-time control. When you create simulations that use statistical signals to control the dynamics, you access the current statistical values at key times throughout the simulation, not just at the end of the simulation.
This table lists SimEvents blocks that output commonly used statistics for data analysis and run-time control.
Block Name | Statistics Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Average queue length/store size, l | Average wait, w | Number of entities arrived, a | Number of entities departed, d | Number of entities extracted, ex | Number of entities in block, n | Number of pending entities, np | Pending entity present in block, pe | Utilization, util | |
| Conveyor System |
|
|
| ||||||
| Entity Batch Creator |
|
|
| ||||||
| Entity Batch Splitter |
|
|
| ||||||
| Entity Find |
|
|
|
| |||||
| Entity Generator |
|
| |||||||
| Entity Queue |
|
|
|
|
| ||||
| Entity Selector |
|
|
| ||||||
| Entity Server |
|
|
|
|
|
|
| ||
| Entity Store |
|
|
|
|
| ||||
| Entity Terminator |
| ||||||||
| Multicast Receive Queue |
|
|
|
|
| ||||
| Resource Acquirer |
|
|
|
| |||||
| Resource Pool |
| ||||||||
The statistical parameters are updated on particular events during the simulation. For example, when a full N-server advances one entity to the next block, the statistical signal representing the number of entities in the block assumes the value N-1. However, if the departure causes another entity to arrive at the block at the same time instant, then the statistical signal assumes the value N. The value of N-1, which does not persist for a positive duration, is a zero-duration value.. This phenomenon occurs in many situations.
This table lists the events that update the block statistics.
| Statistics Port | Updated on Event | ||||
|---|---|---|---|---|---|
| Entry | Exit | Blocked | Preempted | Extracted | |
| Average queue length/store size, l |
|
|
| ||
| Average wait, w |
|
|
| ||
| Number of entities arrived, a |
| ||||
| Number of entities departed, d |
|
| |||
| Number of entities extracted, ex |
| ||||
| Number of entities in block, n |
|
| |||
| Number of pending entities, np |
|
|
| ||
| Pending entity present in block, pe |
|
|
| ||
| Utilization, util |
|
|
|
| |
Average Queue Length and Average Store Size
The formula to compute average queue length or store size
Average queue length, l is the accumulated time-weighted average queue. To compute Average queue length, l at time tf, the block:
Multiplies the size of the queue n by its duration, t = ti - ti-1, to calculate the time-weighted queue.
Sums over the time-weighted queue and averages it over total time tf.
Where:
t is the time between the entity arrival and / or the number of departure events.
f is the total number of entity arrival and / or the number of departure events between t0 and tf.
i = 1 for simulation time t0 = 0.
Average store size, l is computed similarly by replacing the queue length with the store size.
Average queue length example in the Entity Queue block
This example shows the average queue length of the entities in the Entity Queue block.
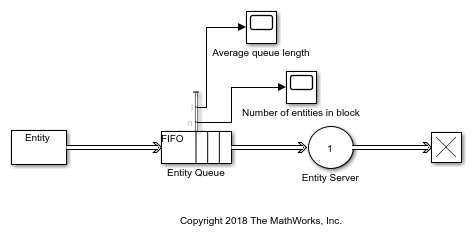
Calculate average queue length in the simple queuing system example
The service time for the Entity Server block is larger than the entity intergeneration time of the Entity Generator block. The entities are queued and sorted in the Entity Queue block. The scope displays the number of entities.
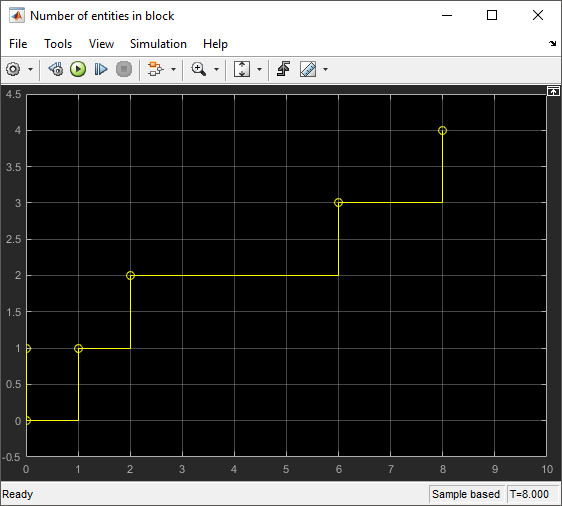
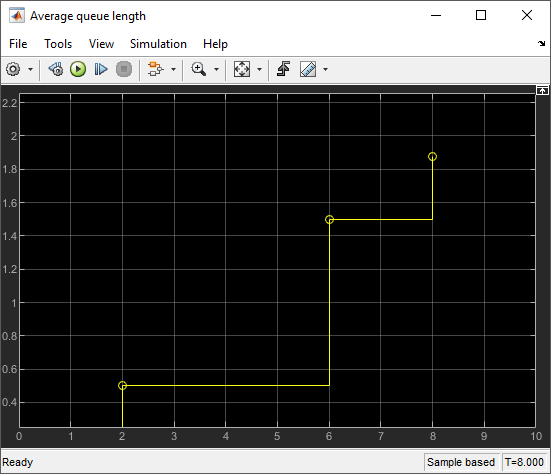
For the duration between 0 and 1, the
average queue length is 0 because the size of the queue is
0. Between 1 and 2
the queue length is 1. Average queue length at time tf = 2 is calculated as follows.
The queue size is 2 between the times 2 and
6 for the duration of 4. Average queue
length at time tf = 6 is calculated using this equation.
The average queue size is calculated for each duration. The Scope block displays its value for the duration of the simulation.
Average Wait
The formula to compute average wait
The Average wait, w parameter represents the sum of the wait times for entities departing the block, divided by their total number, n.
Wait time, wj, is the simulated time that an entity resides within a block.
This wait time is not necessarily equivalent to the time an entity is blocked.
It is the duration between an entity's entry into and exit from a block. For
instance, wait time is 1 for an entity that travels through
an unblocked Entity Server with a service time of
1s.
Average wait of entities example in the Entity Server block
This example shows the average wait time for entities that are served in the Entity Server block.
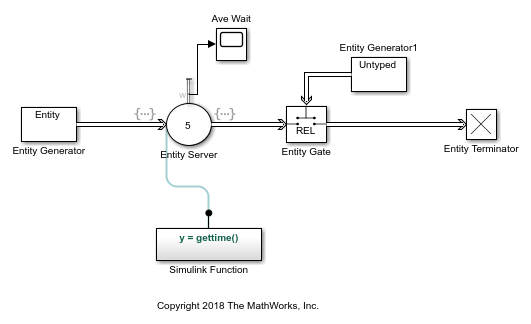
Calculate average wait in the example
The duration of an entity's entry into and exit from the Entity
Server block is computed by the gettime()
function in the Simulink Function block.
The Diagnostic Viewer displays the duration between the entry and exit of six consecutive entities.
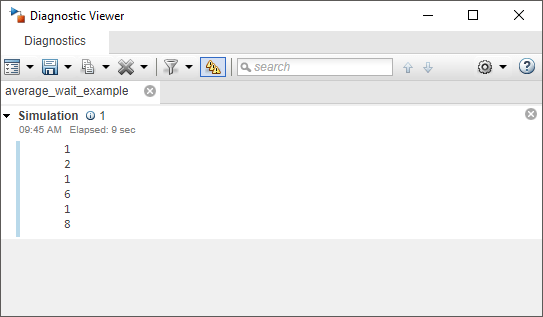
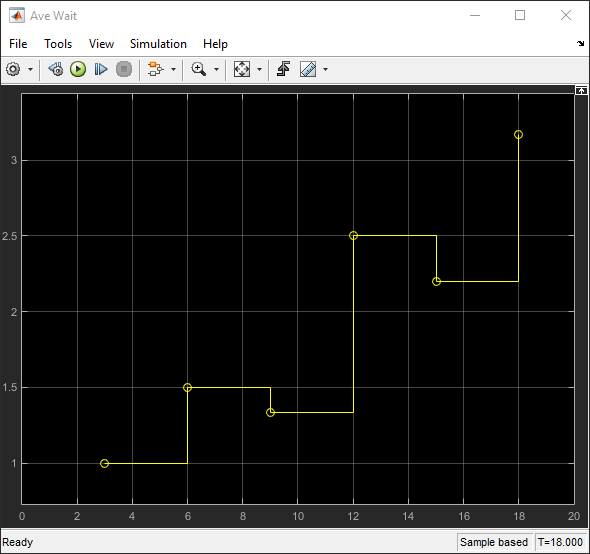
The Scope block shows the average wait time for each entity
departure event from the Entity Server block. For instance, the
wait time for the first entity is 1 and the wait time for the
second entity is 2. The average wait time calculated for the
first two entities is 1.5. The plot displays this value at
the simulation time 6. For the first four entities, the sum
of the wait times is 10 and the average wait time at
simulation time 12 becomes 2.5.
Number of Entities Arrived
The Number of entities arrived, a parameter outputs the cumulative count for the number of entities that arrive at the block.
Number of Entities Departed
The Number of entities departed, d parameter outputs the cumulative count for the number of entities that depart the block.
Number of Entities Extracted
Entity Find block finds entities in a SimEvents model and extracts them from their location to reroute. The Number of entities extracted, ex parameter outputs the number of entities that are extracted from a block.
Number of Entities in Block
The Number of entities in block, n parameter outputs the number of entities that are in the block.
Number of Pending Entities
The Number of pending entities, np parameter outputs the number of pending entities the block has served that have yet to depart.
Pending Entity Present in Block
The Pending entity present in block, pe parameter indicates
whether an entity that is yet to depart is present in the block. The value is
1 if there are any pending entities, and 0
otherwise.
Utilization
The Utilization, util parameter indicates the average time a block is occupied. The block calculates utilization for each entity departure event, which is the ratio of the total wait time for entities to the server capacity, C, multiplied by the total simulation time, tf. Utilization for n entities is calculated using this equation.
References
[1] Cassandras, Christos G. Discrete Event Systems: Modeling and Performance Analysis. Homewood, Illinois: Irwin and Aksen Associates, 1993.
See Also
Entity Server | Entity Generator | Entity Queue | Multicast Receive Queue | Resource Acquirer | Entity Terminator