Main Content

Die Übersetzung dieser Seite ist veraltet. Klicken Sie hier, um die neueste Version auf Englisch zu sehen.

Streudiagramm und Augendiagramm mit MATLAB-Funktionen

Live Script öffnen

Dieses Beispiel veranschaulicht, wie mit Augendiagrammen und Streudiagrammen das Signalverhalten visualisiert werden kann. In diesem Beispiel wird ein QPSK-Signal verwendet, das einen Root-Raised-Cosine-(RRC-)Filter durchläuft.

Streudiagramm

Legen Sie die Parameter für den RRC-Filter, das Modulationsschema und das Plotten fest.

span = 10;          % Filter span
rolloff = 0.2;      % Rolloff factor
sps = 8;            % Samples per symbol
M = 4;              % Modulation alphabet size
k = log2(M);        % Bits/symbol
phOffset = pi/4;    % Phase offset (radians)
n = 1;              % Plot every nth value of the signal
offset = 0;         % Plot every nth value of the signal, starting from offset+1

Erstellen Sie mit der Funktion rcosdesign die Filterkoeffizienten.

filtCoeff = rcosdesign(rolloff,span,sps);

Generieren Sie Zufallssymbole für die Alphabetgröße M.

rng default
data = randi([0 M-1],5000,1);

Wenden Sie die QPSK-Modulation an.

dataMod = pskmod(data,M,phOffset);

Filtern Sie die modulierten Daten.

txSig = upfirdn(dataMod,filtCoeff,sps);

Berechnen Sie das SNR für ein Oversampling-QPSK-Signal.

EbNo = 20;
snr = EbNo + 10*log10(k) - 10*log10(sps);

Fügen Sie AWGN zum übertragenen Signal hinzu.

rxSig = awgn(txSig,snr,'measured');

Wenden Sie den RRC-Empfangsfilter an.

rxSigFilt = upfirdn(rxSig, filtCoeff,1,sps);

Demodulieren Sie das gefilterte Signal.

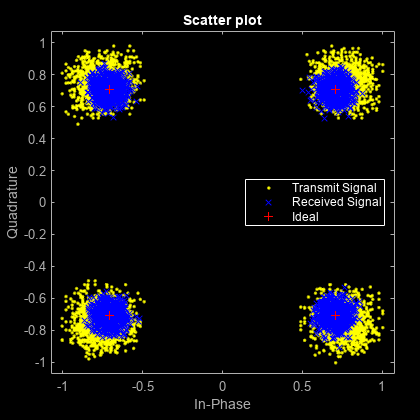
dataOut = pskdemod(rxSigFilt,M,phOffset,'gray');

Verwenden Sie die Funktion scatterplot, um Streudiagramme des Signals vor und nach der Filterung anzuzeigen. Wie Sie sehen, verbessert der Empfangsfilter die Leistung, da die Anordnung den idealen Werten genauer entspricht. Die ersten span-Symbole und die letzten span-Symbole repräsentieren die kumulative Verzögerung der zwei Filteroperationen und werden aus den zwei gefilterten Signalen entfernt, bevor die Streudiagramme generiert werden.

h = scatterplot(sqrt(sps)*txSig(sps*span+1:end-sps*span),sps,offset);
hold on
scatterplot(rxSigFilt(span+1:end-span),n,offset,'bx',h)
scatterplot(dataMod,n,offset,'r+',h)
legend('Transmit Signal','Received Signal','Ideal','location','best')

Figure Scatter Plot contains an axes object. The axes object with title Scatter plot contains 3 objects of type line. These objects represent Transmit Signal, Received Signal, Ideal.

Augendiagramm

Stellen Sie 1000 Punkte des Augendiagramms des übertragenen Signals über zwei Symbolperioden dar.

eyediagram(txSig(sps*span+1:sps*span+1000),2*sps)

{"String":"Figure Eye Diagram contains 2 axes objects. Axes object 1 with title Eye Diagram for In-Phase Signal contains an object of type line. This object represents In-phase. Axes object 2 with title Eye Diagram for Quadrature Signal contains an object of type line. This object represents Quadrature.","Tex":["Eye Diagram for In-Phase Signal","Eye Diagram for Quadrature Signal"],"LaTex":[]}

Stellen Sie 1000 Punkte des Augendiagramms des empfangenen Signals dar.

eyediagram(rxSig(sps*span+1:sps*span+1000),2*sps)

{"String":"Figure Eye Diagram contains 2 axes objects. Axes object 1 with title Eye Diagram for In-Phase Signal contains an object of type line. This object represents In-phase. Axes object 2 with title Eye Diagram for Quadrature Signal contains an object of type line. This object represents Quadrature.","Tex":["Eye Diagram for In-Phase Signal","Eye Diagram for Quadrature Signal"],"LaTex":[]}

Wie Sie sehen, beginnt sich das Augendiagramm des empfangenen Signals aufgrund des Vorhandenseins von AWGN zu schließen. Zudem hat der Filter eine begrenzte Länge, was ebenfalls zu diesem nicht idealen Verhalten beiträgt.

Siehe auch

|

Verwandte Themen