Optimierung des Antriebsstrang-Designs in Bezug auf den Kraftstoffverbrauch mithilfe einer Sensitivitätsanalyse

Für Autokunden in den USA sind Aufkleber wie diese nichts Neues, die sogenannten Monroney-Sticker:

Automobilhersteller müssen diese Sticker in den USA an allen Neufahrzeugen anbringen, damit Kunden wissen, welchen Kraftstoffverbrauch sie erwarten können. Der Kraftstoffverbrauch ist nicht nur ein wichtiger Faktor für Autokäufer, sondern auch ein wesentlicher Punkt für Umweltbehörden, die Normen und Standards festlegen, um die Kraftstoffökonomie in den kommenden Jahren zu verbessern.

Außerdem wurden in jüngster Zeit mehrere Automobilhersteller von Verbrauchern verklagt, weil die Verbrauchszahlen auf dem Monroney-Sticker nicht den realistischen Kraftstoffverbrauch in der Praxis wiedergeben. Die Unterschiede zwischen den Kraftstoffverbrauchszahlen in der Praxis und den Angaben auf Monroney-Stickern haben in den vergangenen Jahren stark zugenommen. Grund hierfür ist, dass die heutigen Kontrollsysteme in den vordefinierten Szenarien, die für Monroney-Kilometerschätzungen verwendet werden, sehr gut abschneiden. Wird das Auto aber bei realistischen Bedingungen gefahren, z.B. bei höheren Geschwindigkeiten auf Fernstraßen, kann sich der Kraftstoffverbrauch stark von der Angabe auf dem Aufkleber unterscheiden. Wie man sich vorstellen kann, interessieren sich Automobilhersteller sehr dafür, welche Konstruktionsentscheidungen getroffen werden können, um die Variabilität des realen Kraftstoffverbrauchs zu reduzieren, indem sie ihre Regelsysteme robuster gegenüber Änderungen der Fahrbedingungen machen.

Daher werden Ingenieure beauftragt zu ermitteln, welche Parameter die größten Auswirkungen auf das Verhalten ihrer Regelungssysteme und den Kraftstoffverbrauch ihrer Fahrzeuge haben. In diesem Artikel beschreiben wir einen interaktiven Workflow, bei dem Monte-Carlo-Simulationen und Sensitivitätsanalyse eingesetzt werden, um zu bestimmen, welche Komponenten im Antriebsstrang eines Autos die größten Auswirkungen auf den Kraftstoffverbrauch haben. Durch die Identifizierung dieser Komponenten können wir Maßnahmen ergreifen, um die erforderlichen Kraftstoffverbrauchswerte zu erzielen. Dazu zählt etwa das Anpassen des Designs zur Reduzierung des Kraftstoffverbrauchs oder das Erhöhen der Robustheit des Regelungssystems gegenüber Veränderungen der Parameter dieser Komponenten.

Der Workflow basiert auf dem Sensitivitätsanalyse-Tool in Simulink Design Optimization™. Wir betrachten dabei einen Pkw mit konventionellem Benzinmotor und berücksichtigen die Unterschiede beim Fahren auf Fernstrecken und im Ortsverkehr. Während dieser Artikel sich auf die Identifizierung von Parametern konzentriert, die sich auf den Kraftstoffverbrauch auswirken, kann der beschriebene Ansatz auch zur Analyse der Sensitivität eines beliebigen Systems verwendet werden, das Schwankungen seiner Designparameter unterliegt.

Systemmodellierung

Um Monte-Carlo-Simulationen und die darauf folgende Sensitivitätsanalyse durchzuführen, benötigen wir zunächst ein Modell, das die Dynamik des Fahrzeugs erfasst und hinsichtlich der verschiedenen Komponenten beschreibt. In unserem Beispiel muss das Modell in Bezug auf die Parameter definiert werden, die sich auf den Kraftstoffverbrauch des Fahrzeugs auswirken können, wie z. B. Antriebsradradius, Übersetzung und Umgebungsbedingungen wie die Temperatur. Wir können dann die Parameter von Interesse in die engere Auswahl nehmen und einen Satz von Parameterkombinationen für Monte-Carlo-Simulationen generieren.

In diesem Beispiel verwenden wir ein Simulink^®-Modell, das im Powertrain Blockset™ verfügbar ist (Abbildung 1). Dieses Modell eines Fahrzeugs mit konventionellem Benzinmotor mit Fremdzündung und 8-Gang-Doppelkupplungsgetriebe umfasst sowohl Umgebungsbedingungen als auch Fahrzeugkomponenten.

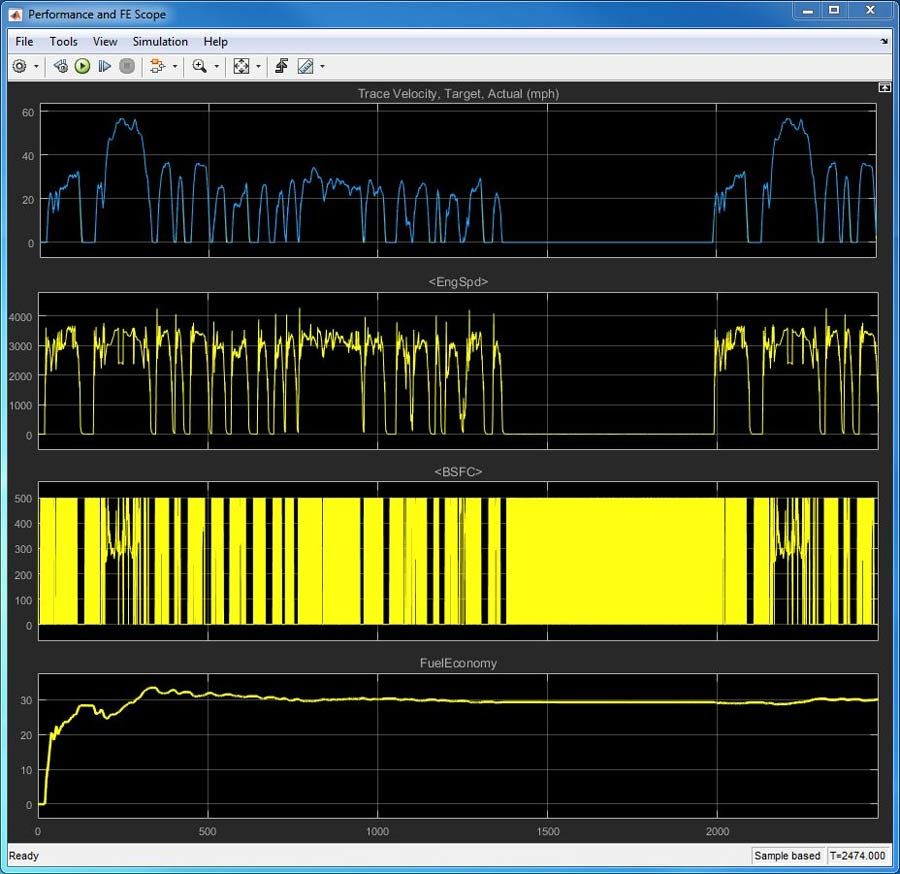
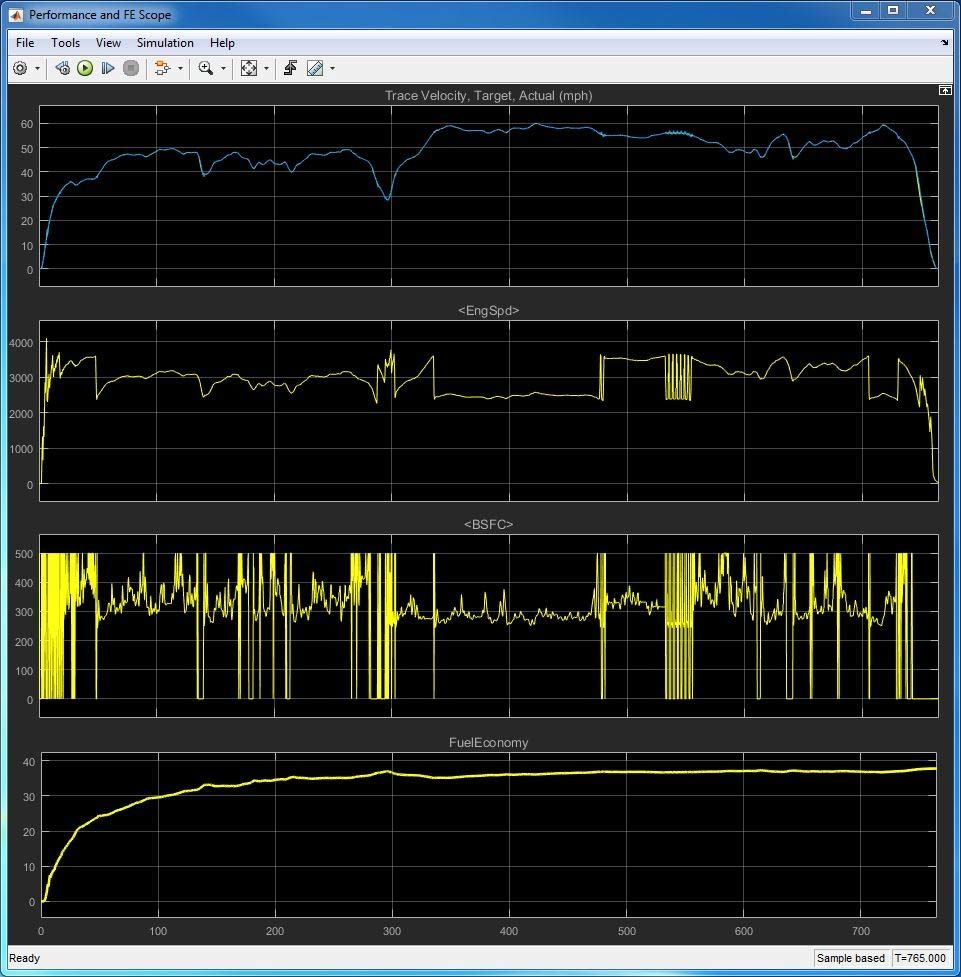
Wir führen zunächst eine Baseline-Simulation mithilfe der FTP75-Fahrzyklusdaten durch, die von der US-Umweltbehörde EPA für Automobilhersteller spezifiziert wurde, die Fahrzeuge in den USA verkaufen. Die Simulationsergebnisse zeigen, dass der Kraftstoffverbrauch für etwa 40 Minuten Stadtverkehr bei circa 30 MPG (Miles per Gallon) liegt (Abbildung 2).

Aufsetzen von Monte-Carlo-Simulationen

Für die Monte-Carlo-Simulationen bestimmen wir die Auswirkungen von fünf Parametern auf den Kraftstoffverbrauch:

• Fahrzeugmasse
• Radradius
• Externer Luftdruck
• Durchmesser der Drosselklappe
• Flussrate der Einspritzdüse

Fahrzeugmasse und Radradius erklären sich von selbst. Der externe Luftdruck bezieht sich auf den Atmosphärendruck der Umgebung. Der Durchmesser der Drosselklappe beeinflusst den Luftstrom in den Motor, während die Flussrate der Einspritzdüse den Kraftstofffluss durch die Einspritzdüsen angibt, was die Motorleistung bestimmt. Variationen im Durchmesser der Drosselklappe und in der Flussrate der Einspritzdüse können durch Abweichungen bei der Komponentenherstellung und Teilealterung wie z. B. „Drosselverkokung“ und Kraftstoffrückstände an der Einspritzdüse verursacht werden. Wir haben uns hier aus Gründen der Einfachheit für einen kleineren Satz von Parametern entschieden, doch kann der Satz erweitert werden und auch Parameter wie die Anzahl der Zylinder, Hubraum und alle im Modell definierten sonstigen Parameter umfassen.

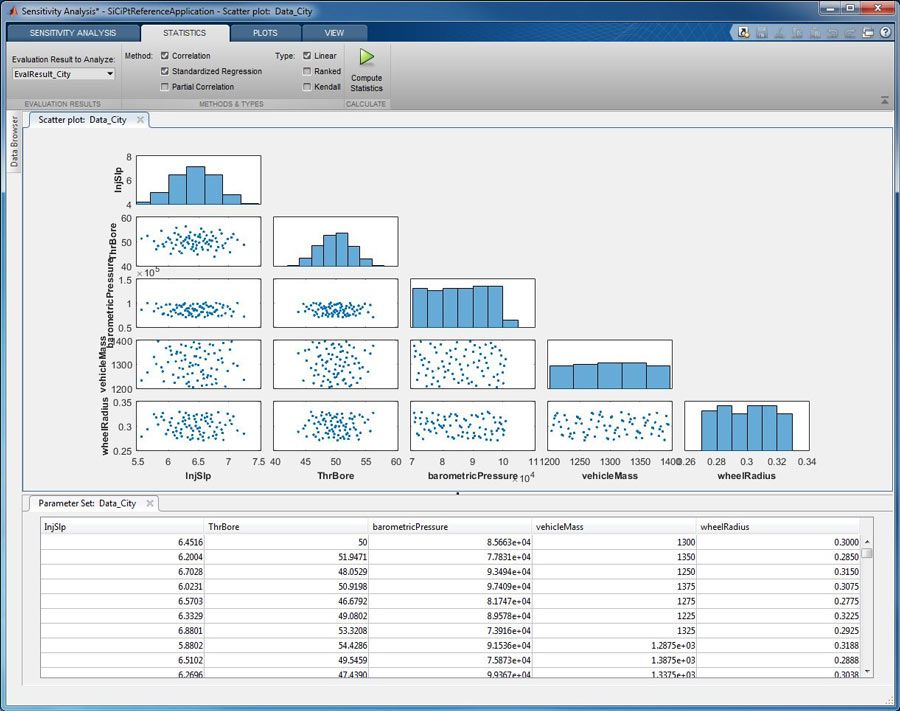
Um einen neuen Parametersatz zu erstellen, der aus den fünf oben angegebenen Parametern besteht, wählen wir im Sensitivitätsanalyse-Tool einfach die Option „Select Parameters“ aus. Dann erstellen wir einen Satz von Parameterkombinationen, der einen Designraum umfasst, der groß genug ist, um zu zeigen, wie sich jeder der fünf Parameter auf den Kraftstoffverbrauch auswirkt. Wir könnten diesen Satz mithilfe fester bekannter Werte erstellen. Wir verwenden hier aber eine quasi-zufällige Folge, eine Sobol-Sequenz, um einen großen Bereich möglicher Kombinationen gleichmäßig und effizient abzudecken. Andere Generierungsmethoden umfassen zufälliges Sampling und multivariates verteilungsbasiertes Sampling.

Wir können die Wahrscheinlichkeitsverteilung angeben, die zur Generierung von Stichproben für jeden Parameter verwendet werden soll, und obere und untere Schranken für die möglichen Werte festlegen. Wir nehmen beispielsweise an, dass die Fahrzeugmasse gleichmäßig zwischen 1200 und 1400 kg verteilt sein soll, was dem Gewicht des Fahrzeugs mit einem bzw. vier Insassen entspricht. Ähnliche Grenzen legen wir für die vier anderen Parameter fest und generieren 100 Kombinationen, die wir dann plotten (Abbildung 3).

Dann wählen wir das Signal in unserem Modell aus, das den Kraftstoffverbrauch für diesen Fahrzyklus (Stadtverkehr) berechnet. In unserem Fall liefert das von uns gewählte Simulink-Signal, das im „Visualization“-Subsystem verfügbar ist, eine kontinuierliche Schätzung des Kraftstoffverbrauchs. Indem wir den letzten Wert dieses Signals betrachten, können wir den MPG-Wert für die jeweilige Simulation schätzen. Dann klicken wir auf die Schaltfläche „Evaluate Model“ im Sensitivitätsanalyse-Tool, um sämtliche Parametersätze zu evaluieren. Das Tool führt eine Simulation des Modells für jede Parameterkombination aus und berechnet den relevanten Wert (in unserem Fall MPG) für jede Simulation. In diesem Modell wird der MPG-Wert durch ein Signal im „Visualization“-Subsystem geschätzt. Wir können dann basierend auf diesen Ergebnissen eine Sensitivitätsanalyse für den MPG-Wert durchführen.

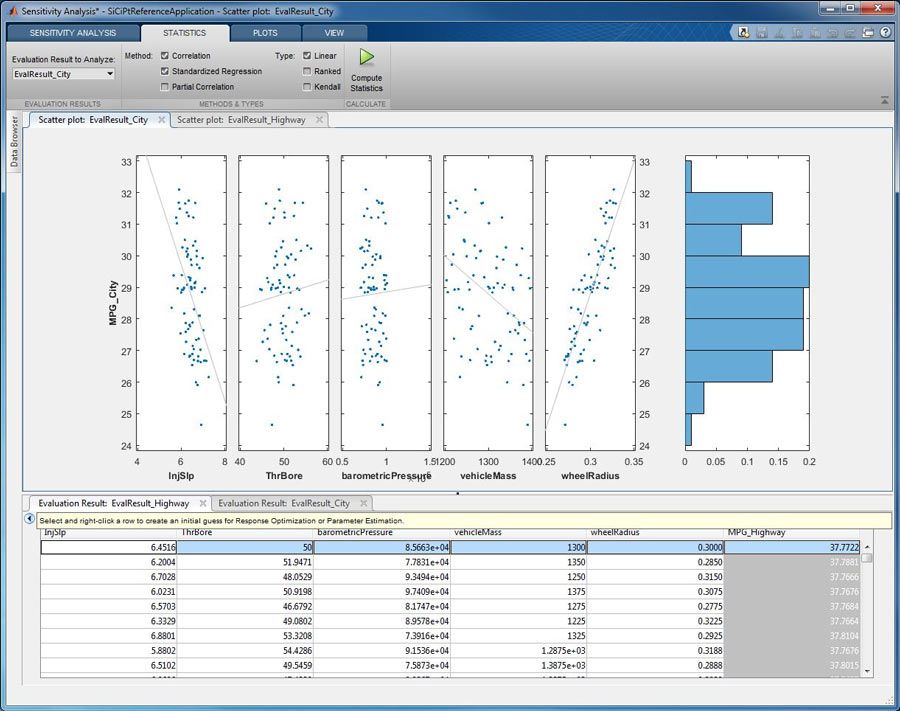
Das Sensitivitätsanalyse-Tool kann parallele Simulationen ausführen, was besonders wichtig ist, wenn wir die große Zahl an Fahrzyklusläufen berücksichtigen müssen, die für die Sensitivitätsanalyse erforderlich sind. Der gegebene Parametersatz wird automatisch parallel von Workern im Cluster evaluiert, mit dem wir eine Verbindung hergestellt haben, und die Ergebnisse werden in einem Streudiagramm visualisiert (Abbildung 4). Die x-Achsen zeigen die Variationen der fünf Parameterwerte an, während die y-Achse den Wert des berechneten Kraftstoffverbrauchs für jede Parameterkombination anzeigt. Das Streudiagramm zeigt, dass der MPG-Wert des Fahrzeugs in unserem Szenario für den gleichen Fahrzyklus zwischen 24 und 32 variieren kann.

Analyse der Sensitivität von MPG bezüglich einzelner Parameter

Wir können eine lineare Anpassung über das Streudiagramm legen, um Trends bei den Simulationsdaten zu identifizieren (Abbildung 5). Daraus erkennen wir, dass der MPG-Wert für den Stadtverkehr sich mit zunehmendem Radradius verbessert. Parallel dazu sehen wir, dass der Kraftstoffverbrauch mit abnehmendem Fahrzeuggewicht sinkt.

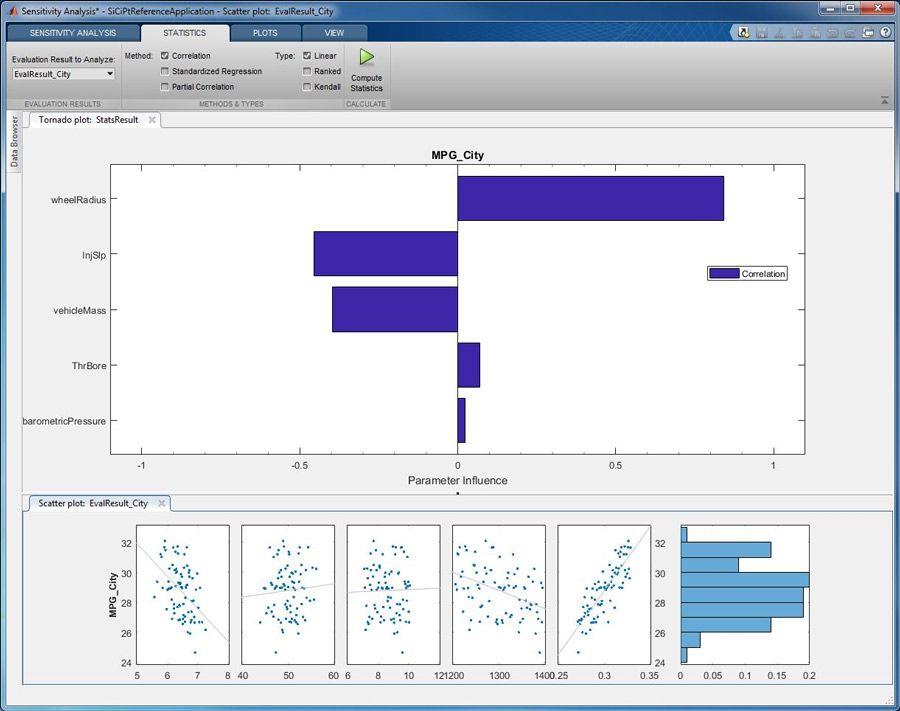
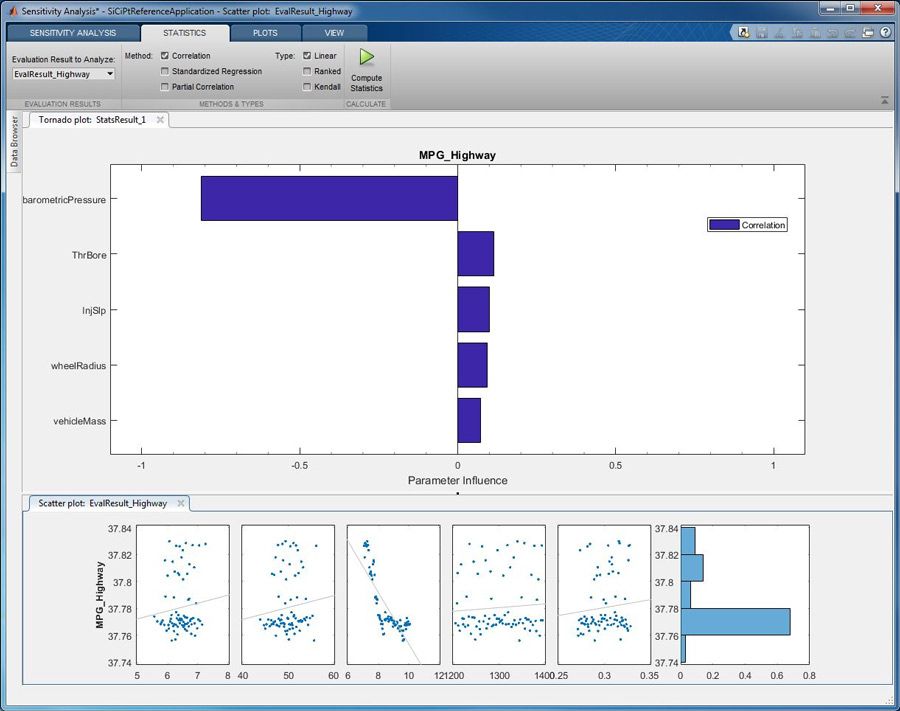
Alternativ können wir die MPG-Sensitivität gegenüber Parametervarianten mithilfe eines statistischeren Ansatzes mit dem Sensitivitätsanalyse-Tool berechnen. Wir können mit dem Tool statistische Werte wie Korrelationskoeffizienten für den MPG-Wert in Bezug auf Parametervariationen berechnen. In diesem Beispiel betrachten wir die Korrelationswerte, die im Tornado-Diagramm in Abbildung 5 dargestellt werden.

Das Diagramm zeigt, dass der MPG-Wert positiv mit dem Radradius und negativ mit der Fahrzeugmasse korreliert. Dies zeigt uns, dass der MPG-Wert bei zunehmendem Radradius und abnehmender Fahrzeugmasse steigt. Anhand der Größe des Balkens im Diagramm, die durch den Korrelationskoeffizienten bestimmt wird, lässt sich erkennen, dass der Einfluss des Radradius auf den MPG-Wert größer ist als der der Fahrzeugmasse. Auf ähnliche Weise verbessert sich der MPG-Wert mit einer Reduzierung der Flussrate der Einspritzdüse. Änderungen des Durchmessers der Drosselklappe und des externen Luftdrucks haben nur sehr geringe Auswirkungen auf den Kraftstoffverbrauch, wie durch ihre niedrigen Korrelationswerte angezeigt wird.

Anschließend betrachten wir, wie das Fahren im Fernverkehr sich auf den Kraftstoffverbrauch auswirkt. Die Simulationsergebnisse für eine 13-minütige Fahrt im Fernverkehr werden in Abbildung 6 dargestellt. Diese Simulation nutzt die von der EPA vorgegebenen HWFET-Fahrzyklusdaten. Als Ergebnis werden circa 35 MPG angezeigt. Wir führen die Monte-Carlo-Simulationen und eine Sensitivitätsanalyse für diesen Fahrzyklus auf der Fernstraße durch, wobei der gleiche Parametersatz wie zuvor verwendet wird. Wie das Tornado-Diagramm für die Korrelationskoeffizienten zeigt, hat der Luftdruck die größten Auswirkungen und der Kraftstoffverbrauch wird bei geringerem Luftdruck reduziert. Die Auswirkungen der anderen Parameter wie Flussrate der Einspritzdüse oder Fahrzeugmasse sind viel geringer (Abbildung 7).

Wie wir sehen können, unterscheiden sich die Auswirkungen der verschiedenen Parameter für die beiden von uns verwendeten Fahrzyklen beträchtlich. Dieser Unterschied kann auf die Tatsache zurückgeführt werden, dass der Motor bei unterschiedlichen Betriebsbedingungen für die verwendeten Fahrzyklen anders läuft. Dies wird durch den Vergleich der Motordrehzahl (zweite Achse) in den Abbildungen 2 und 6 ersichtlich. Die Motordrehzahl hat beim Fahrzyklus in der Stadt mehr Spitzen und Tiefen. Auf der Fernstraße hingegen ist sie gleichmäßiger. Auf größerer Höhe, wo der Atmosphärendruck geringer ist, muss sich das Drosselventil für eine bestimmte Drehzahl weiter öffnen. Das Ergebnis: Weniger Energie geht verloren, wodurch der Kraftstoffverbrauch sinkt. Konsequenterweise sind die Auswirkungen des Luftdrucks auf der Fernstraße viel größer als im Stadtverkehr (Abbildung 7).

Es muss darauf hingewiesen werden, dass diese Ergebnisse stark von den Parameterkombinationen im Datensatz abhängen. Wenn wir die Monte-Carlo-Simulationen für einen engeren Bereich von Radradiuswerten oder einen größeren Bereich von Fahrzeugmassewerten durchführen würden, würde die Sensitivitätsanalyse wahrscheinlich zu anderen Ergebnissen führen.

Verbesserung der Laufzeit von Monte-Carlo-Simulationen mithilfe von Parallelberechnungen

Unser Simulink-Modell weist mehr als 6000 Blöcke auf und enthält Modell-Referenzen, Varianten und Data Dictionaries, die verschiedenen Teams erlauben, das Modell für viele verschiedene Anwendungen einzusetzen. Aufgrund der Größe des Modells ist die Ausführung von hunderten oder tausenden Simulationen auf einem lokalen PC sehr zeitaufwändig. Um die Leistung zu verbessern, führen wir die Simulationen parallel aus. Dazu gibt es mehrere Möglichkeiten: Wir können die Möglichkeit für Parallelberechnungen des Desktops mithilfe der Parallel Computing Toolbox™ nutzen oder auf ein Hochleistungs-Cluster im Netzwerk zugreifen, in dem MATLAB^® ausgeführt wird. In diesem Fall verwenden wir einen 12-Core-Cluster, auf dem MATLAB Parallel Server™ ausgeführt wird und der in einem lokalen Netzwerk verfügbar ist, um die Gesamtsimulationszeit um den Faktor 10 zu reduzieren.

Dazu aktivieren wir einfach die Nutzung unseres Clusters im Menü „Options“ des Sensitivitätsanalyse-Tools. Das Werkzeug sucht dann automatisch die erforderlichen Datei- und Pfadabhängigkeiten und fügt diese hinzu. Dadurch wird sichergestellt, dass jeder parallel arbeitende Worker alle Informationen hat, die er für den erfolgreichen Abschluss der Simulation benötigt.

Zusammenfassung und weitere Schritte

Unsere Analyse zeigt, dass der Radradius im Stadtverkehr den größten Einfluss hat, während sich im Fernverkehr der Luftdruck, also eine Umgebungsbedingung, am stärksten auf den Kraftstoffverbrauch auswirkt.

Einblicke dieser Art machen die Sensitivitätsanalyse zu einem sehr nützlichen Hilfsmittel. Damit können Ingenieure besser verstehen, welche Kompromisse sie berücksichtigen müssen und welche Designänderungen sich am stärksten auf das Systemverhalten auswirken. In diesem Fall können Ingenieure für exakte Angaben auf dem MPG-Sticker beim Autohändler sorgen, indem sie die Regelung um Spezialfunktionen ergänzen und so die Kraftstoffverbrauchswerte Veränderungen der Raddurchmesser gegenüber robuster werden. Wir könnten beispielsweise den Raddurchmesser mittels Raddrehzahlsensoren schätzen und den Getriebeschaltplan ändern, um Durchmesseränderungen zu berücksichtigen und dafür zu sorgen, dass der Motor möglichst effizient arbeitet. Auf ähnliche Weise könnten wir den Kraftstoffverbrauch im Stadtverkehr mithilfe einer größeren Drosselklappe reduzieren.