sin
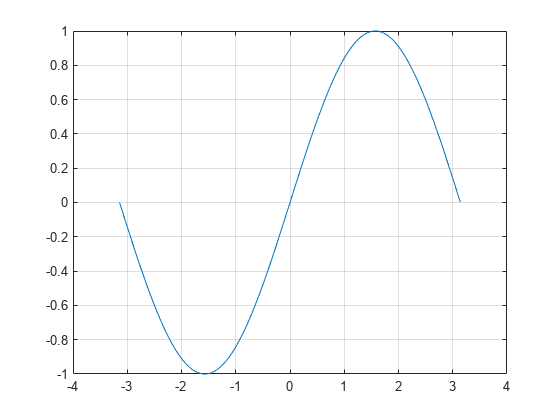
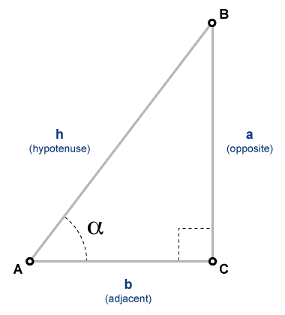
Sinusfunktion eines Arguments in Radiant
Syntax
Beschreibung
Y = sin(X)X zurück. Die Funktion sin führt die Operation für Arrays elementweise durch. Die Funktion akzeptiert sowohl reelle als auch komplexe Eingaben.
Für reelle Werte von
Xgibtsin(X)reelle Werte im Intervall [-1,1] zurück.Für komplexe Werte von
Xgibtsin(X)komplexe Werte zurück.
Beispiele
Eingabeargumente
Ausgabeargumente
Mehr über
Tipps
Um
sin(X*pi)exakt zu berechnen, ohnepials Gleitkomma-Approximation von n zu verwenden, können Sie stattdessen die Funktionsinpiverwenden. Beispielsweise istsinpi(n)genau null für Ganzzahlennundsinpi(m/2)ist +1 oder –1 für ungerade Ganzzahlenm.