Anonyme Funktionen

Was sind anonyme Funktionen?

Eine anonyme Funktion ist eine Funktion, die nicht in einer Programmdatei gespeichert ist, sondern mit einer Variablen verbunden ist, deren Datentyp function_handle ist. Anonyme Funktionen können mehrere Eingaben akzeptieren und geben eine Ausgabe zurück. Sie können nur eine einzige ausführbare Anweisung enthalten.

Hinweis

Sie können eine anonyme Funktion erstellen, die mehrere Ausgaben liefert, indem Sie die Funktion deal verwenden. Ein Beispiel hierfür finden Sie unter Return Multiple Outputs from Anonymous Function.

Erstellen Sie zum Beispiel einen Handle für eine anonyme Funktion, die das Quadrat einer Zahl ermittelt:

sqr = @(x) x.^2;

Die Variable sqr ist ein Function Handle. Der @-Operator erzeugt den Handle, und die Klammern () unmittelbar nach dem @-Operator enthalten die Eingabeargumente der Funktion. Diese anonyme Funktion akzeptiert eine einzelne Eingabe x und gibt implizit eine einzige Ausgabe zurück, ein Array derselben Größe wie x, das die quadrierten Werte enthält.

Finden Sie das Quadrat eines bestimmten Wertes (5), indem Sie den Wert an den Function Handle übergeben, so wie Sie ein Eingabeargument an eine Standardfunktion übergeben würden.

a = sqr(5)

a =
   25

Viele MATLAB^®-Funktionen akzeptieren Function Handles als Eingaben, so dass Sie Funktionen über einen Wertebereich auswerten können. Sie können Handles entweder für anonyme Funktionen oder für Funktionen in Programmdateien erstellen. Der Vorteil der Verwendung anonymer Funktionen ist, dass Sie keine Datei für eine Funktion bearbeiten und pflegen müssen, die nur eine kurze Definition benötigt.

Bestimmen Sie zum Beispiel das Integral der sqr-Funktion von 0 bis 1, indem Sie den Function Handle an die integral-Funktion übergeben:

q = integral(sqr,0,1);

Sie müssen keine Variable im Workspace erstellen, um eine anonyme Funktion zu speichern. Stattdessen können Sie einen temporären Function Handle innerhalb eines Ausdrucks erstellen, wie zum Beispiel diesen Aufruf der integral-Funktion:

q = integral(@(x) x.^2,0,1);

Variablen im Ausdruck

Function Handles können nicht nur einen Ausdruck speichern, sondern auch Variablen, die der Ausdruck zur Auswertung benötigt.

Erstellen Sie zum Beispiel einen Handle für eine anonyme Funktion, die die Koeffizienten a, b und c benötigt.

a = 1.3;
b = .2;
c = 30;
parabola = @(x) a*x.^2 + b*x + c;

Da a, b und c zum Erstellungszeitpunkt von parabola verfügbar sind, enthält der Function Handle diese Werte. Die Werte bleiben innerhalb des Function Handles erhalten, auch wenn Sie die Variablen löschen:

clear a b c
x = 1;
y = parabola(x)

y =
   31.5000

Um unterschiedliche Werte für die Koeffizienten anzugeben, müssen Sie einen neuen Function Handle erstellen:

a = -3.9;
b = 52;
c = 0;
parabola = @(x) a*x.^2 + b*x + c;

x = 1;
y = parabola(x)

y =
   48.1000

Sie können Function Handles und ihre zugehörigen Werte in einer MAT-Datei speichern und sie in einer späteren MATLAB-Sitzung laden, indem Sie die Funktionen save und load verwenden, wie z. B.

save myfile.mat parabola

Verwenden Sie nur explizite Variablen, wenn Sie anonyme Funktionen konstruieren. Falls eine anonyme Funktion auf eine Variable oder eine verschachtelte Funktion zugreift, die nicht explizit in der Argumentliste oder im Funktionskörper referenziert ist, gibt MATLAB einen Fehler aus, wenn Sie die Funktion aufrufen. Implizite Variablen und Funktionsaufrufe finden sich häufig in Funktionen wie eval, evalin, assignin und load. Vermeiden Sie die Verwendung dieser Funktionen im Funktionskörper anonymer Funktionen.

Mehrere anonyme Funktionen

Der Ausdruck in einer anonymen Funktion kann eine andere anonyme Funktion enthalten. Dies ist nützlich, um verschiedene Parameter an eine Funktion zu übergeben, die Sie über einen Wertebereich auswerten. Sie können zum Beispiel die Gleichung

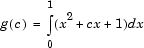
für verschiedene Werte von c durch die Kombination zweier anonymer Funktionen lösen:

g = @(c) (integral(@(x) (x.^2 + c*x + 1),0,1));

So leiten Sie diese Anweisung her:

1. Schreiben Sie den Integranden als anonyme Funktion.

   @(x) (x.^2 + c*x + 1)

2. Werten Sie die Funktion von Null bis Eins aus, indem Sie den Function Handle an integral übergeben.

   integral(@(x) (x.^2 + c*x + 1),0,1)

3. Geben Sie den Wert für c an, indem Sie eine anonyme Funktion für die gesamte Gleichung konstruieren.

   g = @(c) (integral(@(x) (x.^2 + c*x + 1),0,1));

Mit der letzten Funktion können Sie die Gleichung für jeden beliebigen Wert von c lösen. Beispiel:

g(2)

ans =
   2.3333

Funktion ohne Eingaben

Falls Ihre Funktion keine Eingaben erfordert, verwenden Sie leere Klammern, wenn Sie die anonyme Funktion definieren und aufrufen. Beispiel:

t = @() datestr(now);
d = t()

d =
26-Jan-2012 15:11:47

Wenn Sie die Klammern in der Zuweisungsanweisung weglassen, wird ein weiterer Function Handle erstellt und die Funktion nicht ausgeführt:

d = t

d = 
    @() datestr(now)

Funktionen mit mehreren Eingaben oder Ausgaben

Anonyme Funktionen erfordern, dass Sie die Eingabeargumente wie bei einer Standardfunktion explizit angeben und dabei mehrere Eingaben durch Kommas voneinander trennen. Diese Funktion nimmt zum Beispiel zwei Eingaben entgegen, x und y:

myfunction = @(x,y) (x^2 + y^2 + x*y);

x = 1;
y = 10;
z = myfunction(x,y)

z = 
111

Eine anonyme Funktion gibt jedoch nur eine Ausgabe zurück. Wenn der Ausdruck in der Funktion mehrere Ausgaben liefert, können Sie diese anfordern, wenn Sie den Function Handle aufrufen.

Zum Beispiel kann die ndgrid-Funktion so viele Ausgaben zurückgeben, wie es Eingabevektoren gibt. Diese anonyme Funktion, die ndgrid aufruft, gibt nur eine Ausgabe (mygrid) zurück. Rufen Sie mygrid auf, um auf die Ausgaben zuzugreifen, die von der ndgrid-Funktion zurückgegeben werden.

c = 10;
mygrid = @(x,y) ndgrid((-x:x/c:x),(-y:y/c:y));
[x,y] = mygrid(pi,2*pi);

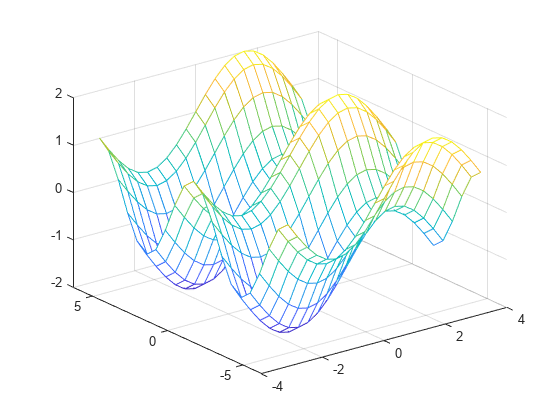
Sie können die Ausgabe von mygrid verwenden, um ein Netz oder ein Oberflächendiagramm zu erstellen:

z = sin(x) + cos(y);
mesh(x,y,z)

Arrays anonymer Funktionen

Die meisten grundlegenden MATLAB-Datentypen unterstützen zwar mehrdimensionale Arrays, die Function Handles müssen aber Skalare (einzelne Elemente) sein. Sie können jedoch mehrere Function Handles in einem Zellen-Array oder Struktur-Array speichern. Der gängigste Ansatz ist die Verwendung eines Zellen-Arrays, wie z. B.

f = {@(x)x.^2;
     @(y)y+10;
     @(x,y)x.^2+y+10};

Denken Sie bei der Erstellung des Zellen-Arrays daran, dass MATLAB Leerzeichen als Spaltentrennzeichen interpretiert. Lassen Sie entweder Leerzeichen in Ausdrücken weg, wie im vorherigen Code gezeigt, oder schließen Sie Ausdrücke in Klammern ein, wie z. B.

f = {@(x) (x.^2);
     @(y) (y + 10);
     @(x,y) (x.^2 + y + 10)};

Greifen Sie mit geschweiften Klammern auf den Inhalt einer Zelle zu. Zum Beispiel gibt f{1} den ersten Function Handle zurück. Um die Funktion auszuführen, übergeben Sie Eingabewerte in Klammern nach den geschweiften Klammern:

x = 1;
y = 10;

f{1}(x)
f{2}(y)
f{3}(x,y)

ans =
     1

ans =
    20

ans =
    21

Siehe auch

Themen

• Erstellen von Function Handles
• Types of Functions
• Indexing into Function Call Results