Improving Simulink Design Optimization Performance Using Parallel Computing
By Alec Stothert, MathWorks and Arkadiy Turevskiy, MathWorks
Estimating plant model parameters and tuning controllers are challenging tasks. Optimization-based methods help to systematically accelerate the tuning process and let engineers tune multiple parameters at the same time. Further efficiencies can be gained by running the optimization in a parallel setting and distributing the computational load across multiple MATLAB® workers—but how do you know when an optimization problem is a good candidate for parallelization?
Using an aerospace system model as an example, this article describes the parallelization of a controller parameter tuning task using Parallel Computing Toolbox™ and Simulink Design Optimization™. Topics covered include setting up an optimization problem for parallel computing, the types of models that benefit from parallel optimization, and the typical optimization speed-up that can be achieved.
Using Parallel Optimization to Tune an HL20 Vehicle Glide Slope Controller
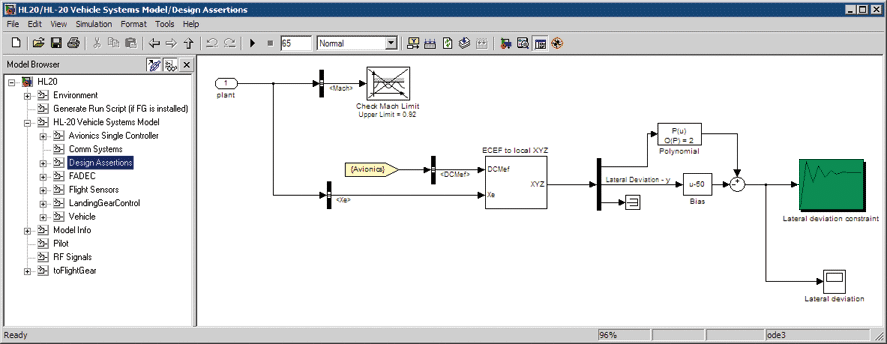
The HL-20 (Figure 1) is a lifting body re-entry vehicle designed to complement the Space Shuttle orbiter. During landing, the aircraft is subjected to wind gusts causing the aircraft to deviate from the nominal trajectory on the runway.
We tune three glide slope controller parameters so as to limit the aircraft’s lateral deviation from a nominal trajectory in the presence of wind gusts to five meters. This task is a good candidate for parallel optimization because the model is complex and takes over a minute to simulate once (optimization can require from tens to hundreds of simulations).
To optimize the controller parameters, we use Simulink Design Optimization (Figure 2).
For comparison, we run the optimization both serially and in parallel1. To run a Simulink Design Optimization problem in parallel, we launch multiple MATLAB workers with the matlabpool command for an interactive parallel computing session2 and enable a Simulink Design Optimization option; no other model configuration is necessary. Figure 3 shows the optimization speed-up when running the HL-20 problem in parallel.
| Optimization algorithm | Dual-core processor (two workers) |
Quad-core processor (four workers) |
||||
|---|---|---|---|---|---|---|
| serial (secs) |
parallel (secs) |
ratio serial:parallel |
serial (secs) |
parallel (secs) |
ratio serial:parallel |
|
| Gradient descent based | 2140 | 1360 | 1.57 | 2050 | 960 | 2.14 |
| Pattern search based | 3690 | 2140 | 1.72 | 3480 | 1240 | 2.81 |
Figure 3. Optimization results for HL-20 controller parameter-tuning problem.
Parallel computing accelerates optimization by up to 2.81 times (the exact speed-up depends on the number of workers and the optimization method used). This is a good result, but notice that the speed-up ratio is not two in the dual-core case or four in the quad-core case, and that the quad-core speed-up is not double the dual-core speed-up. In the rest of the article we investigate the speed-up in more detail.
Running Multiple Simulations in Parallel
Before considering the benefit of solving optimization problems in parallel, let’s briefly consider the simpler issue of running simulations in a parallel setting. To illustrate the effect of parallel computing on running multiple simulations, we will investigate a Monte-Carlo simulation scenario.
Our model, which consists of a third-order plant with a PID controller, is much simpler than the HL20 model. It takes less than a second to simulate, and will help demonstrate the benefits of running many simulations in parallel. The model has two plant uncertainties, the model parameters a1 and a2. We generate multiple experiments by varying values for a1 and a2 between fixed minimum and maximum bounds. The largest experiment includes 50 values for a1 and 50 for a2, resulting in 2500 simulations.
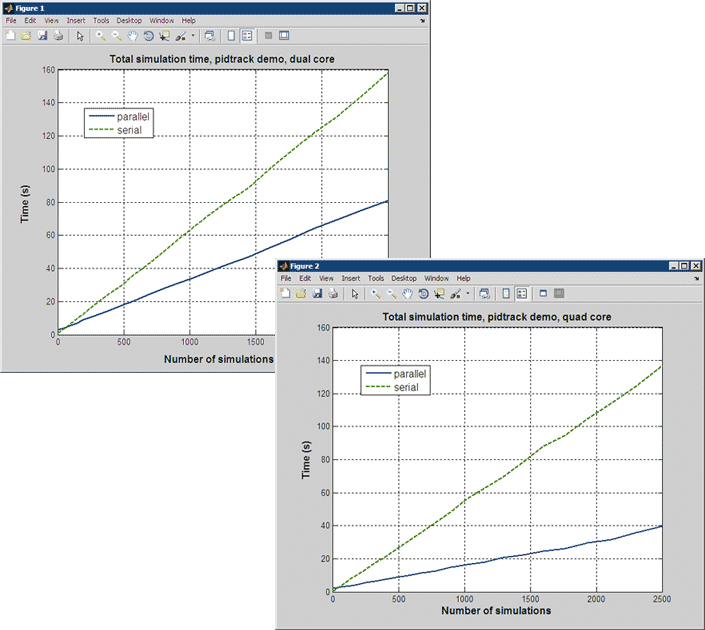
Figure 4 compares the time taken to run multiple experiments of different sizes in serial and parallel settings. The parallel runs were conducted on the same multicore machines that were used in the HL20 example. Network latency, resulting from data transfer between client and workers, did not play a significant role, as inter-process communication was limited to a single machine. We used two worker processes on the dual-core machine, and four on the quad-core machine, maximizing core usage. To optimize computing capacity, the machines were set up with the absolute minimum of other processes running.
The plots in Figure 4 show that the speed-up when running simulations in parallel approaches the expected speed-up: the dual-core experiments using 2 MATLAB workers run in roughly half the time, while the quad-core experiments using 4 MATLAB workers run in roughly a quarter of the time.
Because of the overhead associated with running a simulation in parallel, a minimum number of simulations is needed to benefit from parallel computing. This crossover point can be seen on the extreme left of the two plots in Figure 4. It corresponds to 8 simulations in the dual-core case and 6 in the quad-core case.
The results show clear benefits from running simulations in parallel. How does this translate to optimization problems that run some, but not all, simulations in parallel?
When Will an Optimization Benefit from Parallel Computing?
Many factors influence the effect of parallel computing on speed-up. We will concentrate on the two that affect Simulink Design Optimization performance: the number of parameters being optimized and the complexity of the model being optimized.
Number of Parameters
The number of simulations that an optimization algorithm performs depends on the number of parameters being optimized. To illustrate this point, consider the two optimization algorithms used to optimize the HL20 model: gradient descent and pattern search.
Gradient Descent Optimization
At each iteration, a gradient-based optimization algorithm requires the following simulations:
- A simulation for the current solution point
- Simulations to compute the gradient of the objective at the current design point with respect to the optimized parameters
- Line-search evaluations (simulations to evaluate the objective along the direction of the gradient)
Simulations required to compute gradients are independent of each other, and can be distributed. Figure 5 shows the theoretically best expected speed-up. The plot in Figure 5 shows that the relative speed-up increases as parameters are added. There are four MATLAB workers in this example, giving a potential speed-up limit of 4, but because some of the simulations cannot be distributed, the actual speed-up is less than 4.
The plot also shows local maxima at 4,8,12,16 parameters. These local maxima correspond to cases where the parameter gradient calculations can be distributed evenly among the MATLAB workers. For the HL20 aircraft problem, which has 3 parameters, the quad-core processor speed-up observed was 2.14, which closely matches the speed-up shown in Figure 5. In Figure 5 we kept the number of parallel MATLAB workers constant and increased the problem complexity by increasing the number of parameters.
%We compute the theoretically best expected speedup as follows:
Np = 1:32; %Number of parameters (32 parameters are needed to
%define 8 filtered PID controllers)
Nls = 0; %Number of line search simulations, assume 0 for now
%The gradients are computed using central differences so there
%are 2 simulations per parameter. We also need to include
%the line search simulations to give the total number of
%simulations per iteration:
Nss = 1+Np*2+Nls; %Total number of serial simulations, one nominal,
%2 per parameter and then line searches
%The computation of gradients with respect to each parameter
%can be distributed or run in parallel. Running the gradient
%simulations in parallel reduces the equivalent number of
%simulations that run in series, as follows:
Nw = 4; %Number of MATLAB workers
Nps = 1 + ceil(Np/Nw)*2+Nls; %Number of serial simulations
%when distributing gradient
%simulations
%The ratio Nss/Nps gives us the best expected speed-up
In Figure 6 we increase the number of MATLAB workers as we increase the number of parameters. The plot shows that, if we have enough workers, running an optimization problem with more parameters takes the same amount of time as one with fewer parameters.
% This code is a modification of the code shown in Figure 5.
Nw = Np; %Ideal scenario with one
%processor per parameter
Nps = 1 + ceil(Np/Nw)*2+Nls; %Total number of serial
%simulations--
%in this case, ceil(Np/Nw)=1
%The ratio Nss/Nps gives us the best expected speed-up.
Pattern Search Algorithm
Pattern search optimization algorithms evaluate sets of candidate solutions at each iteration. The algorithms evaluate all candidate solutions and then generate new candidate solution sets for the next iteration. Because each candidate solution is independent, the evaluation of the candidate solution set can be parallelized.
Pattern search uses two candidate solution sets: search and poll. The number of elements in these sets is proportional to the number of optimized parameters:
%Default number of elements in the solution set Nsearch = 15*Np; %Number of elements in the poll set with a 2N poll method Npoll = 2*Np;
The total number of simulations per iteration is the sum of the number of candidate solutions in the search and poll sets. During evaluation of the candidate solutions, simulations are distributed evenly among the MATLAB workers. The number of simulations that can run in series after distribution thus reduces to
Nds = ceil(Nsearch/Nw)+ceil(Npoll/Nw);
When evaluating the candidate solutions in series, the optimization solver terminates each iteration as soon as it finds a solution better than the current solution. Experience suggests that about half the candidate solutions will be evaluated. The number of serial simulations is thus approximately
Nss = 0.5*(Nsearch+Npoll);
The search set is used only in the first couple of optimization iterations, after which only the poll set is used. In both cases, the ratio Nss/Nds gives us the speed-up (Figure 7).
Figure 8 shows the corresponding speed-up when the number of MATLAB workers is increased.
The expected speed-up over a serial optimization should lie between the two curves. Notice that even with only one parameter, a pattern search algorithm benefits from distribution. Also recall that for the HL20 aircraft problem, which has 3 parameters, the quad-core speed-up observed was 2.81, which closely matches the speed-up plotted in Figure 7.
How Simulation Complexity Affects Speed-Up
Our simplified analysis of parallel optimization has taken no account of the overhead associated with transferring data between the remote workers, but this overhead could limit the expected speed-up. The optimization algorithm relies on shared paths to give remote workers access to models, and the returned data is limited to objective and constraint violation values, making the overhead typically very small. We can therefore expect that performing optimizations in parallel will speed up the problem, except when model simulation time is nearly zero. For example, the simple PID model required the distribution of 6 or more simulations to see a benefit. If we were to optimize the three PID controller parameters for this model, there would be 1+2*3+Nls simulations per optimization iteration, and we would not expect to see much benefit from parallelization3.
The Effect of Uncertain Parameters on Parallel Optimization
Optimization must often take account of uncertain parameters (parameters such as the a1 and a2 variables in the simple model, which vary independently of those being optimized). Uncertain parameters result in additional simulations that must be evaluated at each iteration, influencing the speed-up effect of parallelization. These additional simulations are evaluated inside a parameter loop in the optimization algorithm, and can be considered as one, much longer simulation. As a result, uncertain parameters do not affect the overhead-free speed-up calculations shown in Figures 5 – 8, but they have a similar effect to increasing simulation complexity, and reduce the effect of the overhead on parallel optimization speed-up.
Further Possibilities for Optimization Speed-up
Optimization-based methods make plant model parameter estimation and controller parameter tuning more systematic and efficient. Even more efficiency can be gained for certain optimization problems by using parallel optimization. Simulink Design Optimization can be easily configured to solve problems in parallel, and problems with many parameters to optimize, complex simulations with long simulation times, or both can benefit from parallel optimization.
Another way to accelerate the optimization process is to use an acceleration mode in Simulink. Simulink provides an Accelerator mode that replaces the normal interpreted code with compiled target code. Using compiled code speeds up simulation of many models, especially those where run time is long compared to the time associated with compilation. Combining the use of parallel computing with Accelerator simulation mode can achieve even more speed-up of the optimization task.
1 Our setup comprises a dual-core 64-bit AMD®; 2.4GHz, 3.4GB, and quad-core 64-bit AMD; and 2.5GHz, 7.4GB Linux® machines.
2 We use the matlabpool command to launch 2 workers on the dual-core machine and 4 workers on the quad-core machine for an interactive parallel computing session.
3 To configure MATLAB for an interactive parallel computing session, you need to open a pool of MATLAB workers using the matlabpool command. This takes a few seconds,but once you have set up the matlabpool and updated the model, optimizations almost always benefit from parallel computations. The setup needs to be executed only once for your entire parallel computing session.
Published 2009 - 91716v00